Akima
Interpolates a given set of points using Akima spline fitting.
Controller: CodeCogs 
Interface
C++
Class Akima
The original algorithm is based on a piecewise function composed of a set of polynomials, each of degree three, at most,and applicable to successive interval of the given points. In this method, the slope of the curve is determined at each given point locally, and each polynomial representing a portion of the curve between a pair of given points is determined by the coordinates of and the slopes at the points. For more information concerning the algorithm, see references. An important detail when using this class is that the abscissas array given as argument to the constructor needs to be sorted in ascending order. If you initial data represents maximum and minimums and you are concerned about overshoot (or spurious oscillations) then the Akima method is highly recommended. However it is worth noting that if your data points change abruptly then some small overshoot will still arise. Below you will find the interpolation graphs for a set of points obtained by evaluating the function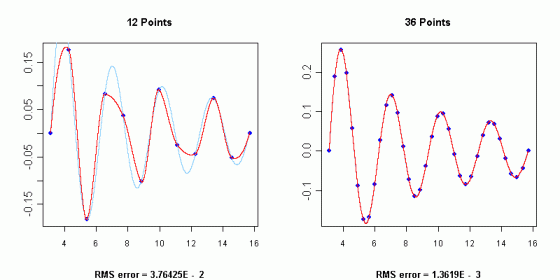
References:
- Hiroshi Akima, "A Method of Bivariate Interpolation and Smooth Surface Fitting for Irregularly Distributed Data Points", ACM Transactions on Mathematical Software, Vol. 4, No. 2, June 1978, pp. 148-159. Copyright 1978, Association for Computing Machinery, Inc., reprinted by permission.
- F.R. Ruckdeschel, "BASIC Scientific Subroutines, Vol. II, BYTE/McGRAWW-HILL, 1981.
- For a general overview of different approaches see: http://www.kxcad.net/CINEMA_4D/help/US/html/OSPLINEFORMULA-ID_OBJECTPROPERTIES.html
Example 1
- The following example displays 20 interpolated values (you may change this amount through
the N_out variable) for the given function
with abscissas equally spaced in the
interval. The X and Y coordinate arrays are initialized by evaluating this function for N = 12 points equally spaced in the domain from
to
.
#include <codecogs/maths/approximation/interpolation/akima.h> #include <math.h> #include <iostream> #include <iomanip> using namespace std; #define PI 3.1415 #define N 12 int main() { // Declare and initialize two arrays to hold the coordinates of the initial data points double x[N], y[N]; // Generate the points double xx = PI, step = 4 * PI / (N - 1); for (int i = 0; i < N; ++i, xx += step) { x[i] = xx; y[i] = sin(2 * xx) / xx; } // Initialize the Akima spline interpolation routine with known data points Maths::Interpolation::Akima A(N, x, y); // Interrogate spline curve to find interpolated values int N_out = 20; xx = PI, step = (3 * PI) / (N_out - 1); for (int i = 0; i < N_out; ++i, xx += step) { cout << "x = " << setw(7) << xx << " y = "; cout << setw(13) << A.getValue(xx) << endl; } return 0; }
Output:x = 3.1415 y = -5.89868e-005 x = 3.63753 y = 0.140177 x = 4.13355 y = 0.181798 x = 4.62958 y = 0.0850367 x = 5.12561 y = -0.129668 x = 5.62163 y = -0.157484 x = 6.11766 y = -0.00477961 x = 6.61368 y = 0.0819989 x = 7.10971 y = 0.0712833 x = 7.60574 y = 0.0445423 x = 8.10176 y = -0.00985429 x = 8.59779 y = -0.0801354 x = 9.09382 y = -0.087151 x = 9.58984 y = 0.0367525 x = 10.0859 y = 0.086111 x = 10.5819 y = 0.0312046 x = 11.0779 y = -0.0221298 x = 11.5739 y = -0.04029 x = 12.07 y = -0.0462165 x = 12.566 y = -0.0233795
See Also
Also consider the regression methods: Regression/Discrete, Regression/Forsythe, Regression/Orthogonal, Regression/StiefelAuthors
- Lucian Bentea (August 2005)
Source Code
Source code is available when you buy a Commercial licence.
Not a member, then Register with CodeCogs. Already a Member, then Login.
Members of Akima
Akima
Initializes the necessary data for following evaluations of the spline.Akima( int n double* x double* y )[constructor] n The number of points x The x-coordinates of the points y The y-coordinates of the points
GetValue
Returns the approximated ordinate at the given abscissa.doublegetValue( double x ) x The abscissa of the interpolation point
Akima Once
| doubleAkima_once( | int | N | |
| double* | x | ||
| double* | y | ||
| double | a | ) |
Example 2
x = 3.1415 y = -5.89868e-005 x = 3.63753 y = 0.140177 x = 4.13355 y = 0.181798 x = 4.62958 y = 0.0850367 x = 5.12561 y = -0.129668 x = 5.62163 y = -0.157484 x = 6.11766 y = -0.00477961 x = 6.61368 y = 0.0819989 x = 7.10971 y = 0.0712833 x = 7.60574 y = 0.0445423 x = 8.10176 y = -0.00985429 x = 8.59779 y = -0.0801354 x = 9.09382 y = -0.087151 x = 9.58984 y = 0.0367525 x = 10.0859 y = 0.086111 x = 10.5819 y = 0.0312046 x = 11.0779 y = -0.0221298 x = 11.5739 y = -0.04029 x = 12.07 y = -0.0462165 x = 12.566 y = -0.0233795
There is an error with your graph parameters for Akima_once with options N=20 x="3.1 3.6 4.1 4.6 5.1 5.6 6.1 6.6 7.1 7.6 8.1 8.5 9.0 9.5 10 10.5 11 11.5 12 12.5" y="0 0.14 0.18 0.09 -0.12 -0.15 -0.004 0.082 0.7 0.45 -0.009 -0.08 -0.087 0.036 0.86 0.0312 -0.022 -0.04 -0.046 -0.02" a=2:12.5 .inputError Message:Function Akima_once failed. Ensure that: Invalid C++
Parameters
N The number of initial points x The x-coordinates for the initial points (evenly spaced!) y The y-coordinates for the initial points a The x-coordinate for the output point
Returns
- the interpolated y-coordinate that corresponds to a.
Source Code
Source code is available when you buy a Commercial licence.
Not a member, then Register with CodeCogs. Already a Member, then Login.


 6.00
6.00

