Or login with:
Curved Beams
An analysis of stresses and strains in curved beams



Springs
An analysis of the common types of engineering springs.
_76_60_thumb.gif)

Struts
An analysis of Struts using the EULER Formula.

Shear Force and Bending Moment
An introduction to Shear Force and Bending Moments in Beams.
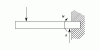
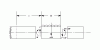
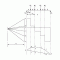

Shear Stress
An introduction Shear Stress, Modulus of Rigidity and Strain Energy.



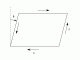
Direct Stress and Strain
Intoduction to terms used in "Materials" and the concepts of Direct Stress and Strain
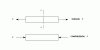
Direct Stress
Resilience and Direct Stress in bars, both composite and of varying cross section.
Compound Stress and Strain part 1
The results of both tensile and shear stress acting together.
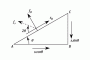
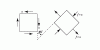
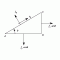
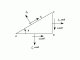
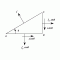
Compound Stress and Strain Part 2
A description of Mohr's Stress and Strain Circles, two and three dimensional Stress and Strain systems, and Strain Energy.
Elastic Constants
Describes the realtionship between the Elastic Constants, and introduces Bulk Modulus and Young's Modulus.
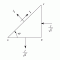
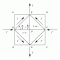
Plastic Theory of Bending
Describes Bending above the yield Stress for elastic materials (Mild Steel).
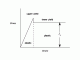

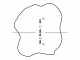

Thick Walled cylinders and Spheres
Analysis of the Stress and Strain in thick walled cylinders, Plastic Yielding and compound Tubes.
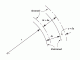
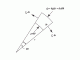


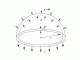
Rotating Discs and Cylinders
The Stresses and Strains generated in a rotating disc or cylinder.
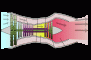
Circular Plates
Stresses and Strains in loaded Circular Plates and Rings.

Notations
A list of the symbols used in our Engineering Materials pages.
 Login
Login
