I have forgotten
my Password

advanced search

Valid RSS

Engineering › Fluid Mechanics › Fundamentals ›

Chezy Equation

Mean flow velocity within pipes with turbulent flow
Contents
  1. Overview
  2. Theory
  3. Page Comments

Overview

The Chezy equation applied to pipes with turbulent flow is

v=C\sqrt{mi}
(1)
where
  • i is \inline \displaystyle \frac{h_f}{l} or head loss due to fiction over the pipe length,
  • m is \inline \displaystyle \frac{A}{P} or wetted area divided by the wetted perimeter,
  • and C is \inline \displaystyle \sqrt{\frac{2g}{f}} where f is the coefficient of friction.

Theory

For the flow of a fluid within a pipe with velocity (v), there will be a reduction in mean pressure with distance, which is usually referred to as "head loss".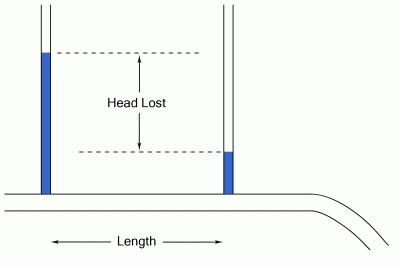

22109/img_0003_13.png
+

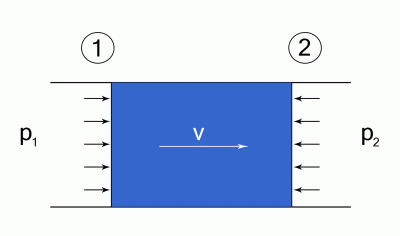
22109/img_0004_11.png
+

Frictional resistance is proportional \inline \frac{1}{2}\:\rho\:v^2 and the wetted area around the circumference of the pipe. Therefore,
H_l=f\:P\:L\:\frac{1}{2}\rho v^2
where
  • P is the perimeter of the pipe \inline =h_1\:A-h_2\:A,
  • L is the length of the pipe section
  • and f is the coefficient of friction

Rearranging
v^2 = \frac{2}{f\rho}\:\frac{A}{P}\:\left( \frac{h_1\:-\:h_2}{l} \right)

\therefore\;\;\;v = C\:\sqrt[]{\mu\:i}
where:
C = \sqrt[]{\frac{2\:w}{f\:\rho}} = \sqrt[]{\frac{2g}{f}}

$m$ =\frac{A}{P}
where m is the hydraulic mean depth

$h$=\frac{m}{l}
where h is the slope of the hydraulic gradient.

Note: C is not a constant since f is a function of Reynolds number
Last Modified: 23 Nov 11 @ 12:27     Page Rendered: 2022-01-17 15:08:05