Engineering › Fluid Mechanics › Notches ›

Triangular Notch

Discharge over a Triangular Notch

Overview

A triangular notch is also called a V-notch. Consider a triangular notch, in one side of the tank, over which water is flowing as shown in figure.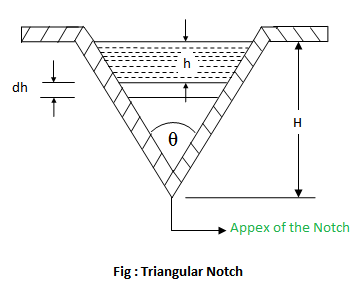

Let,

H = Height of the liquid above the apex of the notch
θ = Angle of the notch
C_d = Coefficient of discharge

From the geometry of the figure, we find that the width of the notch at the water surface,

$= 2H\tan \frac{\theta}{2}$

$\inline \therefore$ Area of the strip = $\inline 2(H-h)\tan \frac{\theta}{2}. dh$

We know that the theoretical velocity of water through the strip = $\inline \sqrt {2gh}$

and discharge over the notch,

$dq = C_d \times Area\;of\;strip \times Theoretical\;velocity$

$\Rightarrow dq = C_d \times 2(H-h)\tan \frac{\theta}{2}. dh\sqrt {2gh}$

The total discharge over the whole notch may be found out only by integrating the above equation within the limits 0 and H.

$Q = \int_{0}^{H} C_d \times 2(H-h)\tan \frac{\theta}{2}. dh\sqrt {2gh}$

$\Rightarrow Q = 2C_d\sqrt {2g}\times \tan \frac{\theta}{2} \int_{0}^{H} (H-h)\sqrt h dh$

$\Rightarrow Q = 2C_d\sqrt {2g}\times \tan \frac{\theta}{2}\int_{0}^{H} (Hh^\frac{1}{2}-h^\frac{3}{2}) dh$

$\therefore Q = \frac{8}{15}C_d \sqrt {2g} \tan \frac{\theta}{2}\times H^{\frac{5}{2}}$

A triangular notch gives more accurate results for low discharges than rectangular notch and the same triangular notch can measure a wide range of flows accurately.

Example:

[metric]

Example - Discharge through a triangular notch

Problem

A right-angled V-notch was used to measure the discharge of a centrifugal pump. If the depth of water at V-notch is 200mm, calculate the discharge over the notch in liters per minute. Assume coefficient of discharge as 0.62.

Workings

Given,

$\inline \theta = 90^{\circ}$
$\inline H = 200\;mm = 0.2\;m$
$\inline C_d = 0.62$

We know that the discharge over the triangular notch,

$Q = \frac{8}{15}C_d \sqrt {2g} \tan \frac{\theta}{2}\times H^{\frac{5}{2}}$

$\Rightarrow Q = \frac{8}{15}\times 0.62\times \sqrt {2\times 9.81} \tan 45^{\circ}\times (0.2)^{\frac{5}{2}}$

$\Rightarrow Q = 1.465\times 0.018 = 0.026 m^3/s$

$\therefore Q = 26\;liters/s = 1560\;liters/min$

Solution

Discharge over the notch = 1560 liters/s

Last Modified: 21 Jan 12 @ 19:16 Page Rendered: 2022-03-14 07:59:15