Engineering › Fluid Mechanics › Orifice › Geometry ›

Submerged Orifice

Discharge through a submerged orifice

View version details

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\tau$ ) = $I\omega\Omega$ (In the limit).

= Moment of Inertia.
$\omega$ = Angular velocity
$\Omega$ = Angular velocity of precession.

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, writer and Catholic philosopher.

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Discharge Through A Wholly Drowned Orifice

When the outlet side of an orifice is beneath the surface of liquid it is known as a wholly submerged orifice as shown in fig.1. In such orifices, the coefficient of contraction is equal to one.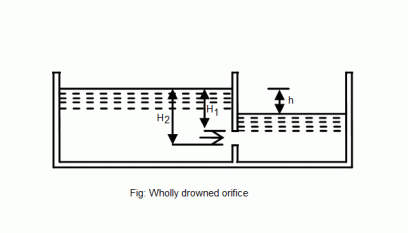

Consider a wholly drowned orifice discharging water as shown in fig.1.

Let,

$H_{1}$ = Height of water (on the upstream side) above the top of the orifice
$H_{2}$ = Height of water (on the upstream side) above the bottom of the orifice
= Difference between the two water levels on either side of the orifice
$C_{d}$ = Coefficient of discharge
$C_{v}$ = Coefficient of velocity
$C_{c}$ = Coefficient of contraction

$\therefore$ Area of orifice = $b(H_{2}-H_{1})$

We know that the theoretical velocity of water through the strip = $\sqrt {2gh}$

$\therefore$ Actual velocity of water = $C_{v}\sqrt {2gh}$

From the relation of hydraulic coefficients we know that, $C_{d} = C_{v}\times C_{c}$

Since coefficient of contraction is 1 in this case, therefore $C_{d} = C_{v}$

$\therefore$ Actual velocity of water = $C_{d}\sqrt {2gh}$

Now the discharge through the orifice,

= Area of orifice $\times$ Actual velocity

$\Rightarrow Q = b(H_{2}-H_{1}) \times C_{d}\sqrt {2gh}$

$\therefore Q = C_{d}.b(H_{2}-H_{1}) \times \sqrt {2gh}$

If depth of the drowned orifice (d) is given instead of $H_{1}$ and $H_{2}$ , then in such cases the discharge through the wholly drowned orifice is:

$Q = C_{d}.b.d.\sqrt {2gh}$

(2)

Example:

[metric]

Example - Discharge through a wholly drowned orifice

Problem

A drowned orifice 1.5m wide and 0.5m deep is provided in one side of a tank. Find the discharge in liters/s through the orifice, if the difference of water levels on both the sides of the orifice be 4m. Take $C_{d}$ = 0.64.

Workings

Given,

= 1.5m
= 0.5m
= 4m
$C_{d}$ = 0.64

$\therefore$ Q = C_{d}.b.d \sqrt {2gh}$

$= 0.64 \times 1.5 \times 0.5 \times \sqrt {2\times 9.84 \times 4}$

$= 0.48 \times 8.859$

Solution

Discharge = 4250 liters/s