Engineering › Fluid Mechanics › Water Pressure ›

Masonry Walls

Water pressure on masonry walls

Overview

Consider a vertical masonry wall having water on one of its sides as shown in figure. Now consider a unit length of the wall. We know that the water pressure will act perpendicular to the wall. A little consideration will show, that the intensity of pressure, at the water level, will be zero, and will increase by a straight line law to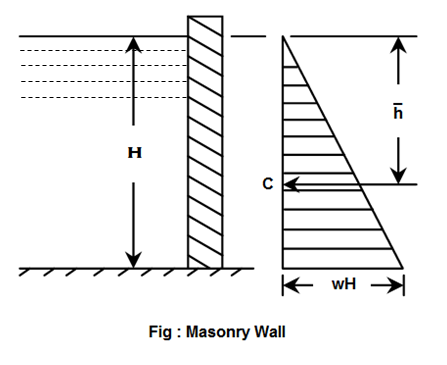 $\inline wH$ at the bottom as shown in figure. Thus the pressure diagram will be a triangle.

The total pressure on the wall will be the area of the triangle, i.e.,

$P = \frac{wH}{2}\times H = \frac{wH^2}{2}$

This pressure will act through the center of gravity of the pressure diagram.

Let, $\inline \bar{h}$ = Depth of the center of pressure from the water surface.

We know that the c.g. of triangle is at a height of $\inline \frac{H}{3}$ from the base, where $\inline H$ is the height of the triangle. Therefore depth of center of pressure from the water surface,

$\bar{h} = H - \frac{H}{3} = \frac{2H}{3}$

Thus the pressure of water on a vertical wall will act through a point at a distance $\inline \frac{H}{3}$ from the bottom, where $\inline H$ is the depth of water.

Example:

[metric]

Example - Water pressure on masonry walls

Problem

One of the walls of a swimming pool contains 4m deep water. Determine the total pressure on the wall, if it is 10m wide.

Workings

Given,

Depth of water, H = 4m
Width of wall = 10m

We know that pressure on the wall per meter length

$= \frac{wH^2}{2} = \frac{9.81\times 4^2}{2} = 78.48\;KN$

and total pressure on the wall,

$P = 10\times 78.48 = 784.8\;KN$

Solution

Total pressure on the wall = 784.8 KN

Last Modified: 25 Feb 12 @ 11:51 Page Rendered: 2022-03-14 17:48:06