Damped and Forced Oscillations

Equations of motion for damped and forced Oscillations

View other versions (2)

Contents

Damped Oscillations.
Forced Oscillations
Page Comments

Damped Oscillations.

Consider the motion of a body in a viscous fluid in which the resistance to motion is proportional to the velocity. Suppose that the body has a weight W and that it is acted upon by a force $\inline \mu\,x$ acting towards x=0 by a constant force F and by a resistance $\inline r\,\dot{x}$ Then applying Newtons Second Law the equation of motion is :

$\frac{W}{g}\;\ddot{x} = F - \mu\,x - r\dot{x}$

(1)

Putting $\inline n^2 = \frac{\mu\;g}{W}$ , $\inline 2k = \frac{r\;g}{W}$ and $\inline b = \frac{F}{\mu}$

The equation of motion can be re-written as:

$\ddot{x} + 2k\,x + n^2(x - b) = 0$

By putting x=b+y

$\ddot{y} + 3k\,\dot{y} + n^2y = 0$

Statical equilibrium occurs when x=b, and y is the displacement from the equilibrium position.

The Auxiliary equation is :

$m^2 + 2km + n^2 = 0$

(2)

The solution of equation therefore takes three forms depending upon whether k < n; k=n or k > n.

If k < n there is slight damping, so

$m= - k\pm j\sqrt{n^2 - k^2}= - k\pm j\,p\;\;\;\;\;\;\;where\;\; p^2 = n^2 - k^2$

Therefore

$y = e^{-kt}(A\cos pt + B\sin pt)$

(3)

and

$x = b + e^{-kt}(A\cos pt + B \sin pt)$

(4)

In this case the body oscillates with a period of $\inline {2\pi}{p}$ . It can also be shown that successive amplitudes form a geometric progression and that the ratio of successive extreme positions on either sides of y=0 is $\inline e^{\frac{-k\pi}{p}$ . In other words the logarithmic decrement of the oscillation is $\inline \frac{k\pi}{p}$ .

If k=n the motion is critically damped and there will be no oscillations. Both roots of the auxiliary equation are equal to -k.

$\therefore\;\;\;\;y = e^{-kt}(A_1 + A_2t)$

(5)

and

$x = b + e^{-kt}(A_1 + A_2t)$

(6)

If k>n the result is a high degree of damping.

$m = -k\,\pm \,\sqrt{k^2 - n^2}$

This can be written as equal to $\inline -\lambda$ and $\inline -\mu$ , hence

$y = A_1\,e^{-\lambda t} + A_2e^{-\mu t}$

(7)

and

$x = b + A_1\,e^{-\lambda t} + A_2e^{-\mu t}$

(8)

As $\inline k \lambda;\;\mu$ are all positive $\inline e^{-kt};\;e^{-\lambda\,t}$ and $\inline e^{-\mu\,t$ will tend to zero as t tends towards infinity. Thus in all three cases as t tends to infinity y tends towards zero and x tends towards b. As a result in case one the oscillations are damped out and the body will ultimately come to rest in its equilibrium position. In the second two cases there will be no oscillations and the body will come to rest in its equilibrium position. In some cases the body may pass through the equilibrium position before returning to it.

Forced Oscillations

If in addition to the force $\inline -\mu\,x$ which causes Simple Harmonic Motion and the force $\inline - r\;\dot{x}$ which causes damping, the body is acted upon by a force $\inline \phi(t)$ the equation of Motion now becomes:

$\frac{W}{g}\ddot{x} = -\mu\,x - r\,\dot{x} + \phi (t)$

(9)

This can be re-written as :

$\ddot{x} + 2k\,\dot{x} + n^2\,x = f(t)$

(10)

where

$f(t) = \frac{g\,\phi \,(t)}{W}$

and k and n have the same meaning as before.

To solve this equation let x=u be a solution of the above equation in which case:

$\ddot{u} + 2k\,\dot{u} + n^2\,u = f(t)$

(11)

Now substitute x= u+z in equation (32)

$\ddot{u} + \ddot{z} + 2k\,\dot{u} + 2k\,\dot{z} + n^2\,u + n^2z = f(t)$

(12)

Subtracting equation (11) from (12)

$\ddot{z} + 2k\,\dot{z} + n^2\,z = 0$

(13)

Thus z is the solution for free damped harmonic oscillations which we have already found in the previous paragraph. Therefore the solution of (10) is obtained by adding together u which is any particular solution and naturally depends upon f(t) and z which is the general solution for free oscillations. i.e. when there is no applied force f(t). We have already seen that the latter is damped out as t increases and hence the solution approaches x=u as t tends towards infinity. For this reason u is called the Steady State and the part z which dies away is called the transient.

In most cases the applied force is either a constant one or it s periodic of period $\inline \frac{2\,\pi}{\omega }$ . In which case f(t) is of the form $\inline a \cos \omega t + b \sin \omega t$ and the steady state can be found by assuming a trial solution $\inline x = A \cos \omega t + B \sin \omega t$ and finding A and B by making the resulting equation identically true, i.e. by making the coefficients of $\inline \cos \omega t$ and $\inline \sin \omega t$ the same on the left hand side of the equation as on the right. This method of finding A and B is shown in the following example.

Example:

[imperial]

Example - Damped Oscillation

Problem

A body which weighs 8 lbs. is acted upon by three forces

6.25x lb.wt acting towards x = 0.
A constant force of 2.5 lbs.wt.
A resistance of $r\,\dot{x}$ .

If $x = 0$ and $dot{x} = 16$ ft/sec at $t = 0$ find x in terms of t when:

r = 0.7
r = 2.5
r = 6.5

Sketch a rough graph of x against t for the three cases.

Workings

By Newton's Second Law the equation of motion is:

$\frac{8}{32} \ddot{x} = 2.5 - 6.25x -r \dot{x}$

(1)

Re-arranging

$\ddot{x} + 4\,r\,\dot{x} + 25(x - 0.4) = 0$

(2)

Let x = 0.4 + y (x = 0.4 is the equilibrium position)

$\therefore\;\;\;\;\ddot{y} + 4\,r\,\dot{y} + 25y = 0$

(3)

First Case

In the first case r = 0.7 so the above equation becomes:

$\ddot{y} + 2.8\,\dot{y} + 25y = 0$

(4)

The resulting auxiliary equation is:

$m^2 + 2.8m + 25 = 0$

(5)

from which $m = -1.4\pm j 4.8$

$\therefore\;\;\;\;x = 0.4 + y = 0.4 + e^{-1.4t}\;(A \cos 4.8 t + B \sin 4.8t)$

(6)

If $x=0$ and $\dot{x} = 16$ at $t=0$

$x = 0.4 + e^{-1.4t}(3.22 \sin 4.8t - 0.4 \cos 4.8t)$

$= 0.4 + 3.24 e^{-1.4t}\sin(4.8t - \alpha)$

(7)

where

$\alpha = 7^0\,5' = 0.124\;\;[rads]$

The Period of the oscillations is:

$\frac{2\pi}{4.8}\approx 1.31\;\;[s]$

Had there been no damping the Period would have been :

$\frac{2\pi}{5}\approx 1.26\;\;[s]$

Second Case

In the second case r = 2.5 and the equation of motion is :

$\ddot{y} + 10\dot{y} + 25\,y = 0$

(8)

The auxiliary equation is $m^2 + 10\,m + 25 = 0$ which has equal roots of -5

$\therefore\;\;\;\;x = 0.4 + e^{-5t}(A_1 + A_2t)$

(9)

If $x = 0$ and $\dot{x} = 16$ at $t = 0$

$x = 0.4 + e^{-5t}(14\;t - 0.4)$

(10)

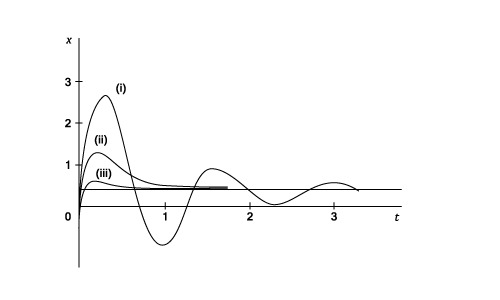
This has one maximum value of approximately 1.3 at t = 0.23

The body will pass through the equilibrium position of x = 0.4 at t = 0.4/14 and then creep back to it again as t tend to infinity.

Third Case

In the third case r = 6.5 and the equations become:

$\ddot{y} + 26\,\dot{y} + 25\,y = 0$

(11)

and

$m^2 - 26m + 25 = 0$

(12)

which has roots m = -1 and m = -25

$\therefore\;\;\;\;x = 0.4 + A_1 e^{-t} + A_2 e^{-25t}$

(13)

If $x=0$ and $\dot{x} = 16$ at $t=0$

$\therefore\;\;\;\;x = 0.4 + 0.25 e^{-t} - 0.65 e^{-25t}$

(14)

This has one maximum value $\approx0.60\;at\;t\;\approx\;0.17$ . The body passes through its equilibrium position when $t\;\approx\,0.4$ and then creeps back to it as t tends to infinity.

Had a smaller initial velocity been taken than 16 ft./sec. it would have been found that when r >2.5 the body would never reach its equilibrium position until t was infinite but that when r <2.5 it would oscillate just as before.

Solution

When r=0.7

When r=2.5

$x = 0.4 + e^{-5t}(14 t - 0.4)$

When r=6.5

$x = 0.4 + 0.25 e^{-t} - 0.65 e^{-25t}$