Maths › Calculus ›

Differentiation

Differentiation of Simple Algebraic Functions from first principles

View other versions (2)

Contents

Differentiation From First Principles
The Differential Coefficient (gradient Function)
The Differentiation 0f A Product Of Two Functions Of X
The Differentiation Of A Product Of Any Number Of Functions Of X
The Differentiation Of A Quotient Of Two Functions Of X
Page Comments

Differentiation From First Principles

It is sometimes required that Differentiation be carried out from first principles.

Consider the following equation

$y=Ax^2+Bx+c$

(1)

Let there be small increase in x of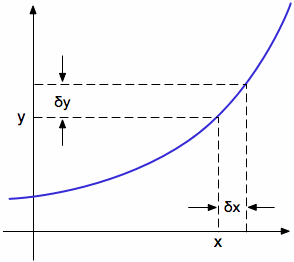 $\delta x$ and let the corresponding increase in y be $\delta y$

Rewriting the original equation

$y+\delta y=A(x+\delta x)^2+B(x+\delta x)+C$

Multiplying out

$y+\delta y=A(x^2+2x\delta x+\delta x^2)+B(x+\delta x)+C$

$y+\delta y=Ax^2+2Ax\delta x+A\delta x^2+Bx+B\delta x+C$

(2)

But we know that

$y=Ax^2+Bx+C$

Subtracting equation (1) from Equation (2)

$\delta y=2Ax\delta x+\delta x^2+B\delta x$

As the value $\delta x$ is reduced and tends towards dx i.e. until it is infinitesimally small, the value of $\delta x ^2$ tends towards zero and can be neglected. $\delta y$ is now written as $dy$ .

It can be seen from the diagram that the value of the tangent at x,y is $\displaystyle \frac{\delta y}{\delta x}$ and at the limit this is written as $\displaystyle \frac{dy}{dx}$

Referring to Equation (1) the value of the tangent is given by:

$\frac{dy}{dx}= 2Ax+B$

The Differential Coefficient (gradient Function)

$\mathbf{\frac{dy}{dx}}$ is known as the Gradient function and represents the Derivative of y with respect of x. It is also known as the b{Differential Coefficient}.

In the simplest case, if

$y=Kx^n+\text{Constant}$

then

$\frac{dy}{dx}=Knx^{n-1}$

Example:

Example - Differentiation

Problem

Find the differentiation of

$y=3x^5+2x^2-5x+6$

Workings

Bringing the power of each x variable down, and subtracting 1 from each power of x yields:

$\frac{dy}{dx}=5\times 3x^{(5-1)}+2\times 2x^{(2-1)}-5x^{(1-1)}$

which is simplified further to

$\frac{dy}{dx}=15x^4+4x-5$

Solution

$\frac{dy}{dx}=15x^4+4x-5$

The Differentiation 0f A Product Of Two Functions Of X

It is obvious, that by taking two simple factors such as 5 X 8 that the total increase in the product is Not obtained by multiplying together the increases of the separate factors and therefore the Differential Coefficient is not equal to the product of the d.c's of its factors. If

$\mathbf{y=uv}$

then

$\mathbf{\frac{dy}{dx}=u\frac{dv}{dx}+v\frac{du}{dx}}$

To Prove the Product Rule let $y=uv$ where u and v are both functions of x. Thus when x increases to $x+\delta x$ u and v will also change to $u+\delta u$ and $v+\delta v$ .

Their product y will therefore become

$(u+\delta u)(v+\delta v)=uv+u\cdot\delta v+v\cdot\delta u+\delta u\;\delta v$

Therefore $\delta y$ , the increase in $y=u \cdot \delta v + v \cdot \delta u + \delta u \cdot \delta v$ Thus

$\frac{\delta y}{\delta x}=u\cdot\frac{\delta v}{\delta x} + v\cdot\frac{\delta u}{\delta x}+\frac{\delta u}{\delta x}\cdot\delta v$

In the limit as $\delta u$ , $\delta v$ and $\delta y$ tend to zero, so the above equation becomes:

$\frac{dy}{dx}=u\;\frac{dv}{dx}+v\;\frac{du}{dx}$

Example:

Example - Differentiation - Product Rule

Problem

Differentiate

$y=(x^3+1)(x^2+2)$

using the Product Rule

Workings

$y=uv$

then the differential is

$\frac{dy}{dx}=u\frac{dv}{dx} + v\frac{du}{dx}$

So for

$y=(x^3+1)(x^2+2)$

$u=x^3+1$

$v=x^2+2$

Thus

$\frac{dy}{dx}=(x^3+1)\cdot 2x+(x^2+2)\cdot 3x^2$

Solution

$\frac{dy}{dx}=5x^4+6x^2+2x$

The Differentiation Of A Product Of Any Number Of Functions Of X

The rule for finding the differential coefficient of a product of two functions of x can be extended to apply to the product of any finite numbers of functions of x If

$y=u\;v\;w$

Where u, v, w are all functions of x, then regarding this as the product of the two factors u and w:

$\frac{dy}{dx}=uv\;\frac{dw}{dx}+w\;\frac{d(uv)}{dx}$

$=uv\:\frac{dw}{dx}+\left ( u\;\frac{dv}{dx}+v\;\frac{du}{dx} \right )$

$=uv\:\frac{dw}{dx}+uw\;\frac{dv}{dx}+vw\;\frac{du}{dx}$

And similarly for any finite number of factors.

Note An important result follows from the above rules. The differential coefficient of $y^2$ with respect to x can be considered to be the product of two factors each of x and hence is given by:

$y\;\frac{dy}{dx}+y\;\frac{dy}{dx}=2y\frac{dy}{dx}$

Similarly, if n is any interger, by taking the product of n factors each of y

$y\;\frac{dy}{dx}+y\;\frac{dy}{dx}=2y\frac{dy}{dx}$

The differential coefficient of $y^n$ With respect to $x=ny^{n-1}\frac{dy}{dx}$

The Differentiation Of A Quotient Of Two Functions Of X

Let

$y=\frac{u}{v}}$

Then

$\frac{dy}{dx}=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}}$

The proof from first principles of the Quotient Rule.

As with previous proofs from first principles x becomes $x+\delta x$ , u becomes $u+\delta$ and v becomes $v+\delta v$ Therefore y becomes $\frac{u+\delta u}{y+\delta y}$ Thus

$\delta y=\frac{u+\delta u}{v+\delta v}-\frac{u}{v}=\frac{v\delta u-u\delta v}{v(v+\delta v)}$