Triangles and Circles

Theorems on Circles and Triangles including a proof of the Pythagoras Theorem

View other versions (2)

Contents

Statements Of Some Theorems On The Circle.
Statements Of Some Theorems On Proportions And Similar Triangles.
Pythagoras Theorem
Two Theorems On Similar Rectilinear Figures.
Page Comments

Statements Of Some Theorems On The Circle.

Theorem A
A straight line drawn from the centre of a circle to bisect a chord which is not a diameter, is at right angles to the chord.

MISSING IMAGE!

22109/pg_1.gif cannot be found in /users/22109/pg_1.gif. Please contact the submission author.

A chord is a line segment joining two points on a circle.

Theorem B
There is only one circle which passes through three given points which are not in a straight line.

Theorem C
Equal chords of a circle are equidistant from the centre and visa versa.

MISSING IMAGE!

22109/pg_2.gif cannot be found in /users/22109/pg_2.gif. Please contact the submission author.

A tangent is a line intersecting the circle at only one point.

Theorem D
The tangent to a circle and the radius through the point of contact are perpendicular to each other.

MISSING IMAGE!

13108/img_pg3.jpg cannot be found in /users/13108/img_pg3.jpg. Please contact the submission author.

Theorem E
The angle which an arc of a circle subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

MISSING IMAGE!

22109/pg_4.gif cannot be found in /users/22109/pg_4.gif. Please contact the submission author.

Theorem F
Angles in the same segment of a circle are equal.

MISSING IMAGE!

22109/pg_5.gif cannot be found in /users/22109/pg_5.gif. Please contact the submission author.

Theorem G
The angle in a semicircle is a right angle.

MISSING IMAGE!

22109/pg_5_1.gif cannot be found in /users/22109/pg_5_1.gif. Please contact the submission author.

Theorem H
The opposite angles of any quadrilateral inscribed in a circle are supplementary.

MISSING IMAGE!

22109/gm_10.gif cannot be found in /users/22109/gm_10.gif. Please contact the submission author.

Theorem I
If a straight line touches a circle and from the point of contact a chord is drawn, the angles which this tangent makes with the chord are equal to the angles in the alternate segment.

MISSING IMAGE!

22109/pg_7.gif cannot be found in /users/22109/pg_7.gif. Please contact the submission author.

Example:

Example - Supplementary

Problem

To Prove
A line $DE$ parallel to the base $BC$ of the triangle $ABC$ cuts $AB$ , $AC$ at $D$ and $E$ respectively. The circle which passes through $D$ and touches $AC$ at $E$ meets $AB$ at $F$ . Prove that $F$ , $E$ , $C$ , $B$ , lie on a circle.

Workings

Construction
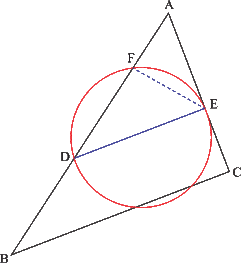
Draw the line $FE$

Proof

$Angle\;CED = Angle\;EFD \;\;\;\;(Theorem\;i)$

Since $DE$ is parallel to $BC$ the angles $CED$ and $BCA$ are supplementary

Hence the angles $BCA$ and $EFD$ are supplementary

Solution

Conclusion
from Theorem H above the points $F$ , $E$ , $C$ , $B$ , lie on a circle.

Statements Of Some Theorems On Proportions And Similar Triangles.

Theorem J
If a straight line is drawn parallel to one side of a triangle, the other two sides are divided proportionally.

MISSING IMAGE!

22109/gm_11.gif cannot be found in /users/22109/gm_11.gif. Please contact the submission author.

Theorem K
If two triangles are equiangular their corresponding sides are proportional.

MISSING IMAGE!

22109/gm_12.gif cannot be found in /users/22109/gm_12.gif. Please contact the submission author.

Theorem L
If two triangles have one equal angle and the sides about these equal angles are proportional, then the triangles are similar.

MISSING IMAGE!

22109/gm_13.gif cannot be found in /users/22109/gm_13.gif. Please contact the submission author.

Theorem M
If a triangle is drawn from the right angle of a right angled triangle to the hypotenuse, then the triangles on each side of of the perpendicular are similar to the whole triangle and to one another.

MISSING IMAGE!

22109/gm_17.gif cannot be found in /users/22109/gm_17.gif. Please contact the submission author.

Theorem N
The internal bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the angle.

MISSING IMAGE!

22109/gm_18.gif cannot be found in /users/22109/gm_18.gif. Please contact the submission author.

Example:

Example - Example 1

Problem

Any line parallel to the base $BC$ of a triangle $ABC$ cuts $AB$ and $AC$ in $H$ and $K$ respectively. $P$ is any point on on a line through $A$ parallel to $BC$ . If $PH$ and $PK$ produced cut $BC$ at $Q$ and $R$ respectively, Prove that $BQ$ = $CR$ .

Workings

Proof

Since AP is parallel to BC

$angle\;HAP = angle\;HBQ\;\;\;\;\;\;\;\;(alternate\; angles)$

$Also \;angle\;BHQ = angle\;PHA$

Hence triangle BHQ is equiangular with triangle APH

$\frac{BQ}{AP} = \frac{BH}{AH}\;\;\;\;\;\;\;\;(similar\;triangles)$

Likewise the triangles APK and KCR are equiangular and hence:-

$\frac{BH}{AH} = \frac{CK}{AK}$

Since HK is parallel to BC, theorem (K) applies and we can write:-

$\frac{BH}{AH} = \frac{CK}{AK}$

Combining the three above equations:-

$\frac{BQ}{AP} = \frac{CR}{AR}$

Solution

Conclusion

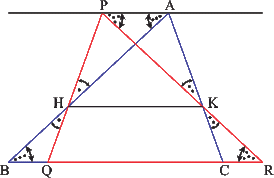
It can be seen that $BQ$ = $CR$ $Q.E.D.$

Pythagoras Theorem

Theorem m provides a convenient method of proving Pythagoras theorem. Consider the right angled triangle $\inline ABC$ .

MISSING IMAGE!

22109/gm_17_1.gif cannot be found in /users/22109/gm_17_1.gif. Please contact the submission author.

Pytagoras theorem
Given the right triangle $\inline \triangle ABC$ prove that $\inline BC^2=AB^2+AC^2$ .

Construction.
Draw $\inline AD$ such that the angle $\inline ADB$ is a right angle.

Proof
The triangles $\inline ABC$ : $\inline ABD$ and $\inline ADC$ are equiangular and similar. From

$\triangle\;ABC\; \sim\triangle\;ADC\;\;\;\;\;\frac{BC}{AC} = \frac{AC}{CD}$

therefore

$AC^2 = BC\times CD$

From

$\triangle\;ABC\;\sim\triangle\;ABD\;\;\;\;\;\frac{BC}{AB} = \frac{AB}{DB}$

therefore

$AB^2 = CB\times DB$

Add equations (22) and (24)

$AC^2 + AB^2 = BC\times CD + BC\times DB = BC\left(CD + DB \right)$

therefore

$\mathbf{AB^2 + AC^2 = BC^2}$

Note
$\inline \sim$ means that the two triangles are similar .

Two Theorems On Similar Rectilinear Figures.

Polygons which are equiangular and have their corresponding sides proportional are said to be similar. If also their corresponding sides are parallel, they are said to be similarly situated (or homothetic)

Theorem 1

The ratio of the areas of similar triangles (or polygons) is equal to the ratio of the squares on corresponding sides.

MISSING IMAGE!

22109/gm_30.gif cannot be found in /users/22109/gm_30.gif. Please contact the submission author.

ABC and PQR are similar triangles and AD and PS are their heights. Since the angle ABD equals angle PQS and the angle BDA equals angle QSP, the triangles ABD and PQS are equiangular and Hence:

$\frac{AD}{PS} = \frac{AB}{PQ} = \frac{BC}{QR}$

The last equality follows from the fact that the triangles ABC and PQR are similar

$\therefore \;\;\;\;\;\frac{\Delta ABC}{\Delta PQR} = \frac{\frac{1}{2}AD\times BC}{\frac{1}{2}PS\times QR} = \frac{BC^2}{QR^2}$

If Polygons are similar they can be divided up into the same number of similar triangles and it follows that the ratio of the areas of similar polygons is equal to the ratio of the squares on corresponding sides.

Theorem 2

If O is any fixed point and ABCD.....P is any polygon and if points A'B'C'.....P' are taken on OA,OB,OC,....OP ( or these lines produced in either direction) such that :

$\frac{OA'}{OA} = \frac{OB'}{OB}\;=....=\frac{OP'}{OP} = \lambda$

Then the polygons ABCD.....P, A'B'C'D'.....P' are similar and similarly situated.

$Since\;\;\;\;\;\;\frac{OA'}{OA} = \frac{OB'}{OB}$

AB is parallel to A'B' and the triangles OAB and OA'B' are similar and hence:

$\frac{A'B'}{AB} = \frac{OA'}{OA} = \lambda$

MISSING IMAGE!

22109/gm_32.gif cannot be found in /users/22109/gm_32.gif. Please contact the submission author.

Corresponding sides of the two polygons are therefore proportional and parallel and the two polygons are similar and similarly situated.

In the above diagram "O" is said to be the centre of similitude of the two polygons. If the corresponding points of the two polygons lie on the same side of O the Polygons are said to be {directly homothetic} with respect to O and O is said to be the external centre of similitude. If the corresponding points lie on opposite sides of O then the Polygons are said to be inversely homothetic with respect to O and O is called the internal centre of similitude.

Example:

Example - Similarities

Problem

$PQR$ is an acute angle triangle. Show how to construct a square with two vertices on $QR$ and one vertex on $PQ$ and one on $PR$ .

Workings

Draw a square $QHKR$ on the other side of $QR$ to the triangle. Join $PH$ and $PK$ and let these lines meet $QR$ at the points $B$ and $C$ respectively. Draw $BA$ and $CD$ perpendicular to $QR$ to meet $PQ$ and $PR$ at the points $A$ and $D$ respectively.

Solution

Then $ABCD$ is the required square for regarding $P$ as the centre of Similitude $ABCD$ is similar to $QHKR$ and is therefore a square.