Engineering › Fluid Mechanics › Machines › Pumps ›

Types

Types of fluid pumps

View other versions (2)

Contents

Types Of Pumps
Vane Type Pump
Equations
Page Comments

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Types Of Pumps

There are two basic categories of pumps:

1. Constant Volume Pumps.

2. Constant Pressure Pumps.

Constant Volume Pumps

Constant volume pumps are also known as Constant Displacement pumps in engineering circles. Amongst Constant Volume pumps, there are four types used in aircraft applications.

a. Gear Type pumps.
b. Vane Type pumps.
c. Gerotor pumps.
d. Piston pumps.

Constant displacement pumps deliver a fixed volume of fluid at low, medium, or high pressure, depending on the needs of the system.

Gear Type Pump

The classic gear type pump is a spur gear arrangement, as illustrated in the diagram alongside. It uses two meshing external tooth gears that fir closely into a figure-eight-shaped housing.

MISSING IMAGE!

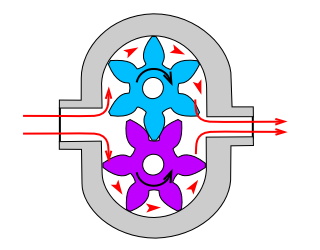
23573/gear_pump.png cannot be found in /users/23573/gear_pump.png. Please contact the submission author.

Vane Type Pump

The vane pump uses two-to-four steel vanes that are free-floating in slots cut in the rotor. As the rotor turns in the direction shown by the arrow, the volume of fluid between the vane and the inlet side of the pump increases, while the volume between the vane and the discharge side of the pump decreases. This change in volume pulls fluid in through the inlet port, and forces fluid out through the discharge port.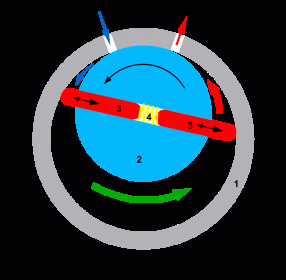

MISSING IMAGE!

23573/612px-rotary_vane_pump_svg.png cannot be found in /users/23573/612px-rotary_vane_pump_svg.png. Please contact the submission author.

Equations

These are a list of randomly created equations. These are not meant for use under any circumstances.

$\sum \alpha \ast \beta \left ( ^{\sum \alpha \ast \beta \left ( ^{}\pi \setminus 2 \right )\kappa = 0}\pi \setminus 2 \right )\kappa = 0$

(2)

$\sum \alpha \ast \beta \left ( ^{}\pi \setminus 2 \right )\kappa = 0$

(3)

From the result obtained in (3), and substituting this in (2), we get

$\sum \alpha \ast \beta \kappa = 0$

(4)