Engineering › Fluid Mechanics › Orifice › Flow From Tanks ›

Circular Horizontal

Time of emptying a circular horizontal tank through an orifice at its bottom

View version details

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, writer and Catholic philosopher.

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Overview

Consider a circular horizontal tank, containing liquid and having an orifice at its bottom as shown in figure.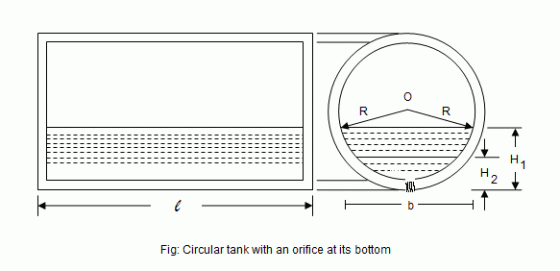

MISSING IMAGE!

23547/circular.png cannot be found in /users/23547/circular.png. Please contact the submission author.

Let,

$\inline R$ = Radius of the tank
$\inline H_{1}$ = Initial height of the liquid
$\inline H_{2}$ = Final height of the liquid
$\inline a$ = Area of the orifice
$\inline l$ = Length of the tank

At some instant, let the height of the liquid be h above the orifice.

We know that the theoretical velocity of the liquid at this instant, $\inline v = \sqrt {2gh}$

At this instant, let b be the breadth of the liquid in the tank.

Then the surface area of the liquid in the tank, $\inline A = l.b$

After a small interval of time dt, let the liquid level fall down by the amount dh.

Therefore volume of the liquid that has passed in time dt,

$dq = A \times (-dh) = -A.dh = -l.b.dh$

(2)

The value of dh is taken as negative, as its value will decrease with the increase in discharge.

We know that the volume of liquid that has passed through the orifice in time dt,

$\inline dq$ = Coefficient of discharge $\inline \times$ Area $\inline \times$ Theoretical velocity $\inline \times$ Time

$\therefore dq = C_{d}.a.\sqrt {2gh}.dt$

(3)

Equating equations (2) and (3)

$-l.b.dh = C_{d}.a.\sqrt {2gh}.dt$

(4)

From the geometry of the tank, we find that,

$\frac{b}{2} = \sqrt {R^2 - (R - h)^2} = \sqrt {R^2 - R^2 + 2Rh - h^2} = \sqrt {2Rh - h^2}$

$\therefore b = 2\sqrt {2Rh - h^2}$

Substituting this value of $\inline b$ in equation (4)

$-l\times 2\sqrt {2Rh - h^2}.dh = C_{d}.a.\sqrt {2gh}.dt$

$\therefore dt = \frac{-2l\sqrt {h(2R-h)}dh}{C_{d}.a.\sqrt {2gh}}$

(5)

Dividing numerator and denominator by $\inline \sqrt h$ ,

$dt = \frac{-2l\sqrt {(2R-h)}dh}{C_{d}.a.\sqrt {2g}} = \frac{-2l(2R-h)^{\frac{1}{2}}dh}{C_{d}.a.\sqrt {2g}}$

Now the total time (T) required to bring the liquid level from $\inline H_{1}$ to $\inline H_{2}$ may be found out by integrating the above equation between the limits $\inline H_{1}$ to $\inline H_{2}$ . Therefore

$T = \int_{H_{1}}^{H_{2}} \frac{-2l(2R-h)^{\frac{1}{2}}dh}{C_{d}.a.\sqrt {2g}}$

$\Rightarrow T = \frac{-2l}{C_{d}.a.\sqrt {2g}}\int_{H_{1}}^{H_{2}}(2R-h)^{\frac{1}{2}}dh$

$\Rightarrow T = \frac{4l}{3C_{d}.a.\sqrt {2g}}[(2R-H_{2})^\frac{3}{2}-(2R-H_{1})^\frac{3}{2}]$

Example:

[metric]

Example - Time of emptying a circular horizontal tank

Problem

An orifice is fitted at the bottom of a boiler drum for the purpose of emptying it. The drum is horizontal and half full of water. It is 10m long and 2m in diameter. Find out the time required empty the boiler, if the diameter of the orifice is 150mm. Assume coefficient of discharge as 0.6.

Workings

Given,