Engineering › Fluid Mechanics › Orifice › Flow From Tanks ›

Transfer

The transfer of liquid from one vessel into another

View version details

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, writer and Catholic philosopher.

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Overview

When two vessels,containing liquid, are connected together by means of an orifice, the liquid will flow from the vessel with a higher level to the vessel with a lower level irrespective of their areas. In such a case the liquid level will fall in one vessel with a corresponding rise in the other. The orifice, through which the flow takes place, is a drowned one and the liquid head causing flow will be the difference between the two liquid levels.

Consider two tanks connected at their bottom by a small orifice as shown in figure.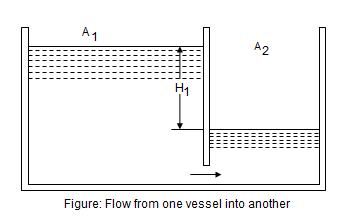

MISSING IMAGE!

23547/one_to_another.png cannot be found in /users/23547/one_to_another.png. Please contact the submission author.

Let,

$\inline A_{1}$ = Area of the larger vessel
$\inline A_{2}$ = Area of the smaller vessel
$\inline a$ = Area of the orifice
$\inline H_{1}$ = Initial difference between the liquid levels of the two vessels
$\inline H_{2}$ = Final difference between the liquid levels of the two vessels
$\inline T$ = Time, in seconds, required to bring the difference of liquid levels from $\inline H_{1}$ to $\inline H_{2}$

At some instant, let the difference between the two liquid levels be h.

The theoretical velocity, $\inline v = \sqrt {2gh}$

After a small interval of time dt, let the liquid level in the vessel $\inline A_{1}$ fall down by an amount equal to x.

$\inline \therefore$ The volume of liquid that has passed from the tank $\inline A_{1}$ = $\inline A_{1}.x$

and the rise of liquid level in the other tank = $\inline \frac{A_{1}}{A_{2}}x$

If the change of liquid level in the tanks be dh in time dt, then

$dh = -(x + \frac{A_{1}}{A_{2}}x)$

(-) negative sign of dh is taken, as the value of h will decrease as the discharge will increase

$\Rightarrow dh = -x(1+\frac{A_{1}}{A_{2}}) = -x(\frac{A_{1}+A_{2}}{A_{2}})$

$\Rightarrow x = \frac{-A_{2}.dh}{A_{1}+A_{2}}$

(2)

In time dt, the volume of water that has passed from tank $\inline A_{1}$

= Coefficient of discharge $\inline \times$ Area $\inline \times$ Theoretical Velocity $\inline \times$ Time

$= C_{d}.a.\sqrt {2gh}\times dt$

(3)

Equating equations (2) and (3),

$A_{1}.x = C_{d}.a.\sqrt {2gh}\times dt$

$\Rightarrow \frac{-A_{1}.A_{2}.dh}{A_{1}+A_{2}} = C_{d}.a.\sqrt {2gh}\times dt$

$\Rightarrow dt = \frac{-A_{1}.A_{2}.dh}{C_{d}.a.(A_{1}+A_{2})\sqrt {2gh}} = \frac{-A_{1}.A_{2}.h^{\frac{1}{2}}.dh}{C_{d}.a.(A_{1}+A_{2})\sqrt {2g}}$

Now the total time (T)required to bring the differences of liquid levels from $\inline H_{1}$ to $\inline H_{2}$ may be found out by integrating the above equation between the limits $\inline H_{1}$ and $\inline H_{2}$ i.e.,

$T = \int_{H_{1}}^{H_{2}} \frac{-A_{1}.A_{2}.h^{-\frac{1}{2}}.dh}{C_{d}.a.(A_{1}+A_{2})\sqrt {2g}}$

$\Rightarrow T = \frac{-A_{1}.A_{2}}{C_{d}.a.(A_{1}+A_{2})\sqrt {2g}}\int_{H_{1}}^{H_{2}}h^{-\frac{1}{2}}dh$

$\Rightarrow T = \frac{-2A_{1}.A_{2}(\sqrt H_{2}-\sqrt H_{1})}{C_{d}.a.(A_{1}+A_{2})\sqrt {2g}}$

Taking minus sign out of the bracket as $\inline H_{1}$ is greater than $\inline H_{2}$

$T = \frac{2A_{1}.A_{2}(\sqrt H_{1}-\sqrt H_{2})}{C_{d}.a.(A_{1}+A_{2})\sqrt {2g}}$

Example:

[metric]

Example - Time of Flow of Liquid from One Vessel into Another

Problem

A tank 6m long and 1.5m wide is divided into two parts, so that area of one part is 7.2m² and that of the other is 1.8m². The water level in the larger part is 3m higher than in the lower one. Find the time taken for difference in water levels to reach 1m if the water flows through a submerged orifice of 75mm diameter, in the partition. Assume coefficient of discharge for orifice as 0.6.

Workings

Given,

Size of the tank = 6 $\times$ 1.5 = 9 m²
$A_{1}$ = 7.2 m²
$A_{2}$ = 1.8 m²
$H_{1}$ = 3m
$H_{2}$ = 1m
$d$ = 75mm = 0.075m
$C_{d}$ = 0.6

We know that the area of the orifice,

$a = \frac{\pi}{4}\times d^2 = \frac{\pi}{4}\times 0.075^2 = 0.0044m^2$

So, time taken for the difference of water levels,

$T = \frac{2A_{1}.A_{2}(\sqrt H_{1}-\sqrt H_{2})}{C_{d}.a.(A_{1}+A_{2})\sqrt {2g}}$

$\Rightarrow T = \frac{2\times 7.2\times 1.8\times (\sqrt 3 - \sqrt 1)}{0.6\times 0.0044\times (7.2 + 1.8)\sqrt {2\times 9.81}}$

$\therefore T = 180\;s = 3\;min$

Solution

Time taken for the difference of water level = 3 min