Engineering › Fluid Mechanics › Pipes ›

Transmission of Power

The transmission of Hydraulic Power through pipelines. Includes Nozzles and Jets, the conditions for maximum Power Transmission , Jet reaction and the efficiency of transmission.

View other versions (5)

Contents

Introduction
Power Transmission In A Pipe
The Conditions For Maximum Power Transmission
Nozzles
The Head Lost In The Nozzle
Efficiency Of The Nozzle
The Nozzle Diameter For Maximum Power Transmission
Jet Reaction
Page Comments

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Introduction

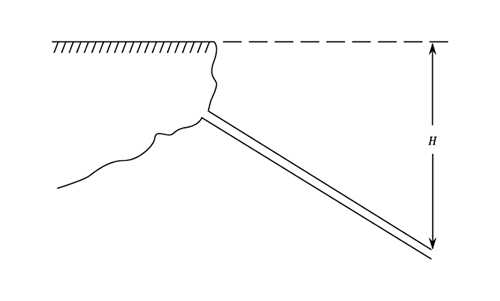
The transmission of power through pipes is both common and widespread in its application. Two examples are the large diameter pipes are used in many hydroelectric schemes and the comparatively small bore pipes used to connect the various pumps; motors and rams used on earth moving plant and machine tools.

Power Transmission In A Pipe

MISSING IMAGE!

23287/transmission_of_power_1.png cannot be found in /users/23287/transmission_of_power_1.png. Please contact the submission author.

A diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle.

Volume is the quantity of three-dimensional space enclosed by some closed boundary.

Power is the rate at which work is done, expressed as the amount of work per unit time and commonly measured in units such as the watt and horsepower.

Water Horse Power is given by:

$\frac{\text{Weight of water / second}\times \text{head}}{550}$

Weight of water / second = $\inline W$

$W\;=\omega\times a\times v$

(2)

Horse Power of a jet is:

$\frac{W\times v^2/2g}{550}=\frac{\omega\times a\times v^3}{2g\times 550}$

(3)

The efficiency of power transmission for the pipe is given by Horse Power at outlet/Horse Power at inlet which is:

$\frac{\displaystyle\frac{W\;v^2/2g}{550}}{\displaystyle\frac{WH}{550}}=\frac{v^2/2g}{H}$

Applying Bernoulli's equation to the pipe and ignoring pipe entry losses:

$H=\frac{v^2}{2g}+h_f$

(4)

Thus the efficiency of Power Transmission can be written as:

$\eta =\frac{H-h_f}{H}$

The Conditions For Maximum Power Transmission

$H=3h_f$

(5)

i.e. The head lost due to friction is one third of the Total Supply Head.

From equations (3) and (4) the Horse Power of the Jet will be:

$\frac{Wv^2/2g}{550}=\frac{W(H-h_f)}{550}$

(6)

The weight of water per second, $\inline W$ , passing down the pipe increases linearly with $\inline v$ , the velocity of the water along the pipe. However $\inline (H-h_f)$ decreases with velocity and there is therefore an optimum velocity which will give the maximum jet Horse Power for a given pipe and Head.

Equation (5) can be rewritten using equation (2). $\inline h-f$ is replaced using the Darcy equation:

$P=\frac{\omega a v}{550}\left ( H-\frac{4flv^2}{2dg} \right )$

$\therefore\;\;\;\;\;P=\frac{\omega a }{550}\left ( Hv-\frac{4flv^3}{2dg} \right )$

For Maximum Power $\inline \displaystyle\frac{dP}{dv}=0$

i.e.

$\frac{\omega a }{550}\left ( H-3\times \frac{4flv^2}{2dg} \right )=0$

From which it can be seen that $\inline H=3h_f$ i.e. The head lost due to friction is one third of the Total Supply Head.

The Efficiency Of Power Transmission For Maximum Power

This is given by:

$\frac{H-\tfrac{1}{3}H}{H}=66.7\%$

The condition for Maximum Power transmitted is rarely used in practice since:

The efficiency of transmission is low and that means that water is wasted;
The velocity in the pipeline is high and this can give rise to dangerous Water Hammer effects when valves are closed.

For these reasons it is normal to limit water velocity to a maximum of 6 ft./sec.

Nozzles

A nozzle is a device designed to control the direction or characteristics of a fluid flow as it exits an enclosed chamber or pipe via an orifice.

MISSING IMAGE!

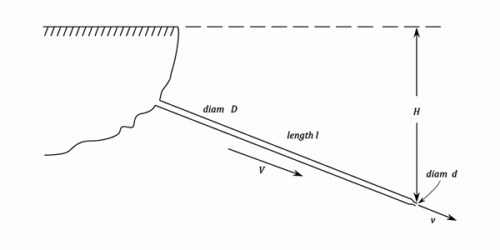
23287/transmission_of_power_2.png cannot be found in /users/23287/transmission_of_power_2.png. Please contact the submission author.

It is assumed that the Head H is the head behind the nozzle and that all pipeline and valve losses have been accounted for elsewhere. There are, of course, losses in the nozzle itself and the actual velocity of discharge will be less than the theoretical value by one to five percent. This is catered for by the use of the coefficient of velocity, $\inline C_V$ , the coefficient of contraction, $\inline C_C$ and the coefficient of Discharge, $\inline C_D$ :

$C_V = \frac{\text{Actual Velocity}}{\text{Theoretical Velocity}}$
$C_C = \frac{\text{Actual cross sectional area}}{\text{Geometric cross sectional Area}}$
$C_D = C_C\times C_V$

MISSING IMAGE!

23287/img_0001_6.png cannot be found in /users/23287/img_0001_6.png. Please contact the submission author.

The Head Lost In The Nozzle

$H_l = \frac{V^2}{2\,g}\left (\frac{1}{{C_{V}}^{2}} - 1 \right )$

(7)

Let $\inline H$ = total head at nozzle (i.e. the sum of the pressure and velocity heads)

$H=H_1- P$

(8)

where $\inline P$ are the Pipe line losses.

$V^2 = {C_{V}}^{2}\;2\,g\,H$

$H = \frac{V^2}{{C_{V}}^{2}\;2\,g}$

Head behind the Nozzle = Head after the nozzle + Head lost in Nozzle:

$H = \frac{v^2}{2g} + H_l$

, where $\inline H_l$ is the head lost.

Substituting from (4) above:

$\therefore\:H_l = H-C_{v}^{2}\:H$

The Head lost in nozzle will be:

$H_l= H (1 - {C_{v}}^{2})$

Or:

$H_l = H(1 - {C_{V}}^{2}) = \frac{V^2}{{C_{V}}^{2}\times2\,g}\left (1 - {C_{V}}^{2} \right )$

$\therefore \;\;\;\;\;\;\;H_l = \frac{V^2}{2\,g}\left (\frac{1}{{C_{V}}^{2}} - 1 \right )$

Efficiency Of The Nozzle

Efficiency ,

$\eta = \frac{v^2}{2g\:H}$

where $\inline H$ is the Head behind nozzle.

$\eta=\frac{C_v\; \sqrt{2g\:H}}{2g\,H} = C_v^2$

Thus:

$C_V=\sqrt\eta$

The Nozzle Diameter For Maximum Power Transmission

$\frac{d}{D}=\sqrt[4]{\frac{D}{8fl}}$

In the following calculations the losses in the nozzle are ignored. Two proofs are given. The first uses the previous result for the power transmission through a Pipe Line and the second is from first principles.

Diagram from notes.

a) It has been shown that the maximum Power transmission through a pipe lie occurs when the head lost due to friction is a third of the total head.

Hence:

$h_f=\frac{1}{3}H$

Or:

$\frac{v^2}{2g}=\frac{2}{3}H=2h_f$

$\therefore \;\;\;\;\;\;\frac{v^2}{2g}=2\times \frac{4flv^2}{2dg}$

$\therefore \;\;\;\;\;\left ( \frac{v}{V} \right )^2=\frac{8fl}{d}$

But:

$d^2v=D^2V$

Or:

$\frac{v}{V}=\left ( \frac{D}{d} \right )^2$

$\therefore \;\;\;\;\;\left ( \frac{D}{d} \right )^4=\frac{8fl}{D}$

Thus:

$\frac{d}{D}=\sqrt[4]{\frac{D}{8fl}}$

b) from first principles

Applying Bernoulli's equation across the nozzle and neglecting losses:

$H=\frac{4flV62}{2gD}+\frac{v^2}{2g}$

And using the continuity equation:

$VD^2=vd^2$

(9)

$H=\frac{4fl}{D}\times \left ( \frac{d}{D} \right )^4\times \frac{v^2}{2g}+\frac{v^2}{2g}= \frac{v^2}{2g}\left [ \frac{4fl}{D}\left ( \frac{d}{D} \right )^4+1 \right ]$

$\therefore \;\;\;\;\;v=\sqrt{\frac{2gH}{\frac{4fl}{D}\times \left ( \frac{d}{D} \right )^4}+1}$

The power output of the nozzle is given by:

$P=\frac{\omega\;a\;v^3}{2g\times 550}$

(10)

$=\frac{\omega\;\pi d^2}{4\times 2g\times 550}\left ( \frac{2gH}{\displaystyle\frac{4fl}{D}\times \left ( \displaystyle\frac{d}{D} \right )^4}+1 \right )^{\frac{3}{2}}$

$=Kd^2\left ( \frac{4fl}{D}\times \left ( \frac{d}{D} \right )^4+1 \right )^{-\frac{3}{2}}$

The nozzle diameter for the maximum power transmission will occur when $\inline \displaystyle\frac{dP}{d(d)}=0$

i.e.

$2d\left [ \frac{4fl}{D}\times \left ( \frac{d}{D} \right )^4+1 \right ]^{-\frac{3}{2}}=\frac{3}{2}d^2\left [ 4fl\left ( \frac{d}{D} \right )^4+1 \right ]^{-\frac{5}{2}}\times 4\times \frac{4fl}{D}\times \frac{d^3}{D^4}$

Multiply both sides by

$\left [ \frac{4fl}{D}\times \left ( \frac{d}{D} \right )^4+1 \right ]^{\frac{5}{2}}$

$\therefore\;\;\;\;\; \frac{4fl}{D}\times \left ( \frac{d}{D} \right )^4+1=\frac{3}{2}\times \frac{d\times 2\times 4fld^3}{D^5}=\frac{12\times fl}{D}\left ( \frac{d}{D} \right )^4$

Or:

$\frac{8fl}{D}\;\left ( \frac{d}{D} \right )^4=1$

$\therefore \;\;\;\;\;\frac{d}{D}=\sqrt[4]{\frac{D}{8fl}}$

Jet Reaction

The jet reaction is the backward force exerted on the nozzle and the pipe and is equal and opposite to the force exerted by the jet on a fixed plate.

i.e. The jet reaction = the mass of fluid passing through the jet per second $\inline X$ the change in velocity.

Therefore the Jet Reaction will be

$\frac{wav^2}{g}$

Nozzle Diameter For Maximum Jet Reaction

$h_f=\left ( \frac{v}{V} \right )^2\times \frac{V^2}{2g}$

Equation (9) shows that:

$v=\sqrt{\frac{2gH}{\displaystyle\frac{4fl}{D}\times \left ( \displaystyle\frac{d}{D} \right )^4+1}}$

Thus the jet reaction, $\inline R$ can be written as:

$R=w\times \frac{\pi}{4}d^2\left ( \frac{2H}{\displaystyle\frac{4fl}{D}\times \left ( \displaystyle\frac{d}{D} \right )^4+1} \right )$

(11)

The maximum jet reaction will occur when:

$\frac{dR}{d(d)}=0$

$\therefore \;\;\;\;\;2d\left [ \frac{4fl}{D}\times \left ( \frac{d}{D} \right )^4+1 \right ]^{-1}=d^2\left [ \frac{4fl}{D}\times \left ( \frac{d}{D}^4+1 \right ) \right ]^{-2}\times \frac{4\times 4fld^3}{D\times D^4}$