Reversible Processes

An analysis of thermodynamically reversible processes, also discussing the work done in a reversible process

View other versions (2)

Contents

Overview
Work Done In A Reversible Process
Page Comments

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Overview

Definitions

Working substance (WS) = the WS is used as the carrier of heat energy. The state of the WS is defined by the values of its properties, e.g. pressure, volume, temperature, internal energy, enthalpy. These properties are also sometimes called functions of state.

<br/>

Key facts

A thermodynamic process is reversible if it may be reversed by some infinitely small change in the conditions affecting it.

Because of the conditions which it must satisfy, no practical process can be considered thermodynamically reversible.

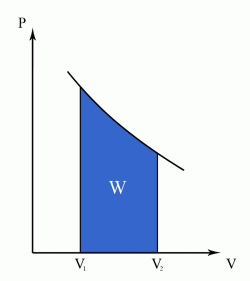
The work done in a reversible process, following a change in volume from $\inline V_1$ to $\inline V_2$ , is given by:

$W = \int_{V_1}^{V_2} P \delta V$

where $\inline P$ is the pressure.

A thermodynamic process is reversible if it may be reversed by some infinitely small change in the conditions affecting it. When reversed, it will pass back through each stage it assumed in the direct sense, and it will have the same state at each point in the direct and reverse process. Therefore, an equal amount of work will be absorbed in the reverse process as is given out in the direct process, and also an equal amount of heat will be rejected in the reverse process as was supplied during the direct process.

In order to be reversible, a thermodynamic process must satisfy certain conditions. For example, a thermodynamic process can not be reversible if:

there is heat transfer between bodies of different temperatures;
there is friction between moving parts, since friction always represents a loss;
there are intermolecular forces;
there are eddies or turbulence in the working substance (WS), since these are irreversible.

From these conditions it can be seen that no practical process can be considered thermodynamically reversible.

Work Done In A Reversible Process

Imagine that the WS is enclosed in a frictionless cylinder with piston, and is initially characterized by the volume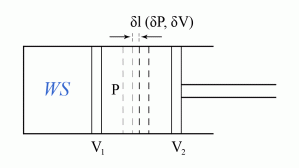 $\inline V_1$ . Now consider that a certain process is performed which changes the volume of the WS to $\inline V_2$ (see Figure 1).

MISSING IMAGE!

746/img_th6.png cannot be found in /users/746/img_th6.png. Please contact the submission author.

Assume that the piston is found at some point where the pressure is $\inline P$ . Let it then move a small distance $\inline \delta l$ , and let the corresponding drop in pressure be $\inline \delta P$ . As the initial pressure is $\inline P$ , and the final pressure $\inline P-\delta P$ , the mean pressure $\inline \bar{P}$ can be calculated as:

$\bar{P} = \frac{P+P-\delta P}{2}$

(2)

from which:

$\bar{P} = P - \frac{\delta P}{2}$

(3)

Taking into account that the force acting on a piston can be written as:

$F = P \cdot A$

(4)

and also considering the expression of the mean pressure from (3), we get that:

$F = \left( P - \frac{\delta P}{2} \right) \cdot A$

(5)

As the work done can be defined as:

$W = F \cdot l$

(6)

and also taking into account (5), we obtain the work done $\inline \delta W$ as a result of the movement of the piston with $\inline \delta l$ :

$\delta W = \left( P - \frac{\delta P}{2} \right) A \cdot l$

(7)

which can also be written as:

$\delta W = \left( P - \frac{\delta P}{2} \right) \delta V$

(8)

or, furthermore, as:

$\delta W = P \delta V - \frac{\delta P}{2} \delta V$

(9)

where $\inline \delta V$ is the change in volume (see Figure 1).

The total work done between volumes $\inline V_1$ and $\inline V_2$ then becomes:

$W = \lim_{\delta V \to 0} \sum_{V_1}^{V_2} P \delta V$

(10)

Consider the corresponding $\inline PV$ plot diagramed in Figure 2.

MISSING IMAGE!

746/img_th7.png cannot be found in /users/746/img_th7.png. Please contact the submission author.

In this plot, the term $\inline P \delta V$ represents the area of the blue shaded infinitesimal strip. When $\inline \delta V \to 0$ , the sum of all such infinitesimal strips between $\inline V_1$ and $\inline V_2$ will equal the area under the curve (the blue shaded area in Figure 3).

MISSING IMAGE!

746/img_th7-2.png cannot be found in /users/746/img_th7-2.png. Please contact the submission author.

Therefore, the total work done can also be written as:

$W = \int_{V_1}^{V_2} P \delta V$

(11)