Built in Beams II

Shear and Deflection formulae for Built in and Continuous Beams.

View other versions (4)

Contents

Introduction
Fixed At Both Ends. Uniform Load. Total Load W
Fixed At Both Ends. Load At Centre.
Fixed At Both Ends. Load At Any Point.
Continuous Beam With Two Equal Spans. Uniform Load
A Continuous Beam With Two Unequal Spans And Unequal Uniform Loads.
A Continuous Beam With Two Unequal Spans With Two Unequal Loads At Any Point On Each
Page Comments

Introduction

See Also the section on "Built in Beams" .

Revisiting the definition, a Beam is said to be Built-in or 'encastre' when both ends are rigidly fixed so that the slope at both ends can be assumed to be zero.

In this section we present the solutions for the stress and deflection in a built in and continuous beam due to either uniform or point loads.

With each solution the following definitions apply:

is the bending at any point
is the section module of the beam cross-section, equal to $Z=\frac{I}{y}$ where is the distance from the beam centroid to the top or bottom edge of the beam.
is the deflection at any point
is the load on the beam
is the modulus of elasticity
is the moment of inertia for the cross section about the neutral axis

Fixed At Both Ends. Uniform Load. Total Load W

The stress at any Point : $S = \displaystyle\frac{W\;l}{2\;Z}\left\{\displaystyle\frac{1}{6} - \displaystyle\frac{x}{l} + \left(\displaystyle\frac{x}{l} \right)^2\right\}$

The Maximum Stress is at the ends and is $\hat{S} = \displaystyle\frac{W\;l}{12\;Z}$

The Stress is zero at $\displaystyle x = 0.7887\;l$ and $x = 0.2113\;l$

The Greatest negative Stress is at the centre and is $\displaystyle S_c\;= - \frac{W\;l}{24\;Z}$

The Deflection at any Point is given by $y = \displaystyle\frac{W\;x^2}{24\;E\:I\;l}\;\;(l - x)^2$

The Maximum Deflection is at the Centre and is $\hat{y} = \displaystyle\frac{W\;l^3}{384\;E\;I}$

Deflection is a term that is used to describe the degree to which a structural element is displaced under a load.

Fixed At Both Ends. Load At Centre.

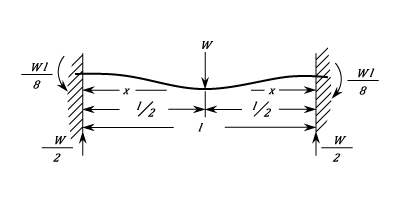
The Stress between each end and the Load: $S = \displaystyle\frac{W}{2\;Z}\;\;\left(\displaystyle\frac{1}{4}\;l - x \right)$

The Stress at each end is : $S_e = \displaystyle\frac{W\;l}{8\;Z}$

The Stress at the middle is: $S_m\;= - \displaystyle\frac{W\;l}{8\;Z}$

These are the maximum Stresses and are equal and opposite.

The stress is zero at $\displaystyle x = \frac{1}{4}\;l$

The Deflection at any point is given by: $y = \displaystyle\frac{W\;x^2}{48\;E\;I}\;\;(3l - 4x)$

The Maximum Deflection is at the Load and is: $\displaystyle \hat{y} = \frac{W\;l^3}{192\;E\;I}$

Fixed At Both Ends. Load At Any Point.

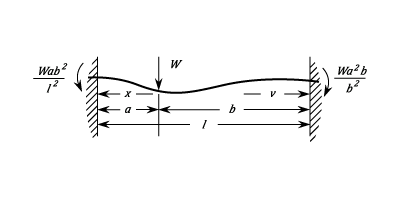
The Stress at any Point within the segment of length

$S_a = \frac{W\;b^2}{Z\;l^3}\;\;\left(al - x[l + 2a] \right)$

The Stress at any point within the segment of length

$S_b = \frac{W\;a^2}{Z\;l^3}\;\;\left(bl - v[l + 2b] \right)$

The Stress at the end next to segment of length

: $S = \displaystyle\frac{W\;a\;b^2}{Z\;l^2}$

The Stress at the end next to segment of length

: $S = \displaystyle\frac{W\;a^2\;b}{Z\;l^2}$

The Maximum Stress is at the end next to the shorter segment.

The Stress is Zero for: $x = \displaystyle\frac{a\;l}{l + 2\;a}$ and $v = \displaystyle\frac{b\;l}{l + 2\;b}$

The Greatest negative stress is at the Load and is given by: $S\;= - \displaystyle\frac{2\;W\;a^2\;b^2}{Z\;l^3}$

The Deflection for the segment of length

is given by:

$y = \frac{W\;x^2\;b^2}{6\;E\;I\;l^3}\;\;2a(l - x) + l(a - x)$

The Deflection for the segment of length

is given by:

$y = \frac{W\;v^2\;a^2}{6\;E\;I\;l^3}\;\;2b(l - v) + l(b - v)$

The deflection at the Load is: $y = \displaystyle\frac{W\;a^3\;b^3}{3\;E\;I\;l^3}$

Let

be the length of the longer segment and

the shorter one.

The Maximum Deflection is in the longer Segment and occurs at $\displaystyle v = \frac{2\;b\;l}{l + 2\;b}$

$\hat{y} = \frac{2\;W\;a^2\;b\63}{3\;E\;I\;(l + 2\;b)}$

Continuous Beam With Two Equal Spans. Uniform Load

A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.

The Stress at any Point is given by: $s = \displaystyle\frac{W\;(l - x)}{2\;Z\;l}\;\;\left(\displaystyle\frac{1}{4}l - x \right)$

The Maximum Stress is at Point

and is: $\hat{S} = \displaystyle\frac{W\;l}{8\;Z}$

The Stress is zero at $\displaystyle x = \frac{1}{4}l$

The greatest negative Stress is at $\displaystyle x = \frac{5}{8}\;l$ and is: $y\;= - \displaystyle\frac{9}{128}\;\;\displaystyle\frac{W\;l}{Z}$

The Deflection at any Point is given by: $y = \displaystyle\frac{W\;x^2\;(l - x)}{48\;E\;I\;l}\;\;(3l - 2x)$

The Maximum Deflection is at $\displaystyle x = 0.5785\;l$ and is given by: $\hat{y} = \displaystyle\frac{W\;l^3}{185\;E\;I}$

The Deflection at the centre of each Span is: ${y} = \displaystyle\frac{W\;l^3}{192\;E\;I}$

The Deflection at the point of greatest negative Stress at $x = \displaystyle\frac{5}{8}\;l$ is ${y} = \displaystyle\frac{W\;l^3}{187\;E\;I}$

A Continuous Beam With Two Unequal Spans And Unequal Uniform Loads.

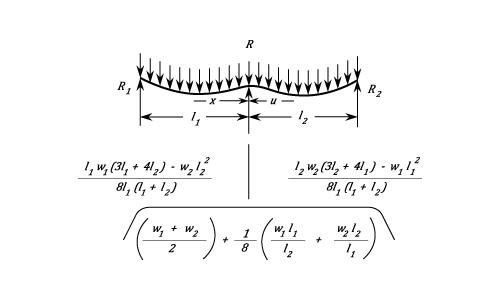
Between $\displaystyle R_1$ and

The Stress is given by: $S = \displaystyle\frac{l_1 - x}{Z}\left\{\displaystyle\frac{(l_1 - x)\;W_1 }{2\;l_1} - R_1\right\}$

Between $\;R_2$ and

The Stress is given by: $S = \displaystyle\frac{l_2 - u}{Z}\;\left\{\displaystyle\frac{(l_2 - u)\;W_2}{2\;l_2} - R_2\right\}$

Stress at the Support

is: $S_R = \displaystyle\frac{W_1\;l_1^2 + W_2\;l_2^2}{8\;Z\;(l_1 + l_2)}$

The greatest Stress in the first span is at: $x = \displaystyle\frac{l_1}{W_1}\;\;(W_1 - R_1)$

And is $\displaystyle \frac{R_1^2\;l_1}{2\;Z\;W_1}$

The greatest Stress in the second Span is at: $u = \displaystyle\frac{l_2}{W_2}\;\;(W_2 - R_2)$

And is $\displaystyle - \frac{R_2^2\;l_2}{2\;Z\;W_2}$

The Deflection between $R_1 \;and\; R$ is given by:

$y = \frac{x(l_1 - x)}{24\;E\;I}\left\{(2l_1 - x)(4R_1 - W_1) - \frac{W_1\;(l_1 - x)^2}{l_1} \right\}$

The Deflection between $R_2\; and \;R$ is given by:

$y = \frac{u(l_2 - u)}{24\;E\;I}\left\{(2l_2 - u)(4R_2 - W_2) - \frac{W_2\;(l_2 - u)^2}{l_2} \right\}$

The above example is so complicated that convenient general expressions for the maximum deflections cannot be obtained

Between point

and the Load the Stress at any Point is: $S = \displaystyle\frac{W}{16\;Z}\;\;(3\;l - 11\;x)$

Between Point

and the Load the stress at any Point $S\;= - \displaystyle\frac{5}{16}\;\;\displaystyle\frac{W\;v}{Z}$

The Maximum Stress at Point

$\hat{S} = \displaystyle\frac{3}{16}\;\;\displaystyle\frac{W\;l}{Z}$

The Stress is Zero at: $x = \displaystyle\frac{3}{11}\;l$

The greatest negative Stress is at the centre of the Span and is:

$\hat{S}_{-ve}\;= - \frac{5}{32}\;\;\frac{W\;l}{Z}$

Between Point

and the Load the Deflection at any point is:

$y = \frac{W\;x^2}{96\;E\;I}\;\;(9\;l - 11\;x)$

Between Point

and the Load the Deflection at any point is:

$y = \frac{W\;v}{96\;E\;I}\;\;(3\;l^2 - 5\;v^2)$

The Maximum deflection at $\displaystyle v = 0.4472$ is: $\hat{y} = \displaystyle\frac{W\;l^3}{107.33\;E\;I}$

The Deflection at the Load is: $y_w = \displaystyle\frac{7}{768}\;\;\displaystyle\frac{W\;l^3}{E\;I}$

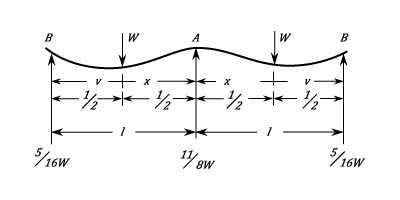
A Continuous Beam With Two Unequal Spans With Two Unequal Loads At Any Point On Each

Between $\displaystyle R_1$ and

the Stress is: $S\;= - \displaystyle\frac{w\;r_1}{Z}$

Between $\displaystyle R$ and

the Stress is: $S = \displaystyle\frac{1}{l_1\;Z}\;\;[m(l_1 - u) - W_1\;a_1\;u]$

Between $\displaystyle R$ and

the Stress is: $S = \displaystyle\frac{1}{l_2\;Z}\;\;[m(l_2 - x) - W_2\;a_2\;x]$

Between $\displaystyle R_2$ and

the Stress is: $S\;= - \displaystyle\frac{v\;r_2}{Z}$

Stress at the Load: $S\;= - \displaystyle\frac{a_1\;r_1}{Z}$

Where,

$m = \frac{1}{2(l_1 + l_2)}\;\;\left(\frac{w_1\;a_1\;b_1}{l_1}\;(l_1 + a_1) + \frac{w_2\;a_2\;b_2}{l_2}\;\;(l_2 + a_2) \right)$

Stress at Support

: $S_R = \displaystyle\frac{m}{Z}$

Stress at load

: $S\;= - \displaystyle\frac{a_2\;r_2}{Z}$

The greatest of these is the maximum Stress.

The Deflection between $\displaystyle R_1$ and

$y = \frac{w}{6\;E\;I}\;\left\{(l_1 - w)(l_1 + w)r_1 - \frac{W_1\;b_1^3}{l_1} \right\}$

The Deflection between $\displaystyle R$ and

$y = \frac{u}{6\;E\;I\;l_1}\;\;[W_1\;a_1\;b_1(l_1 + a_1) - W_1\;a_1\;u^2 - m(2\;l_1 - u)(l_1 - u)]$

The Deflection between $\displaystyle R$ and

$y = \frac{x}{6\;E\;I\;l_1}\;\;[W_2\;a_2\;b_2(l_2 + a_2) - W_2\;a_2\;x^2 - m(2\;l_2 - x)(l_2 - x)]$

The Deflection between $\displaystyle R_2$ and

$y = \frac{v}{6\;E\;I}\;\left\{(l_2 - v)(l_2 + v)r_2 - \frac{W_2\;b_2^3}{l_2} \right\}$

The Deflection at Load $\displaystyle W_1$ : $y = \displaystyle\frac{a_1\;b_1}{6\;E\;I\;}\;[2a_1\;b_1\;W_1 - m(l_1 + a_1)]$

The Deflection at Load $\displaystyle W_2$ : $y = \displaystyle\frac{a_2\;b_2}{6\;E\;I\;}\;[2a_2\;b_2\;W_2 - m(l_2 + a_2)]$