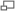Built in Beams

The bending of Built in Beams fixed at both ends.

View other versions (4)

Contents

Introduction
Moment-area Method For Built In Beams
Macaulay Method
Page Comments

Introduction

A Beam is said to be Built-in or 'encastre' when both ends are rigidly fixed so that the slope remains horizontal - It is normal for both ends to be at the same level. In other words, it is assumed that built in beams have zero slope at each end, and therefore the total change of slope along the span is zero.

In general terms, all other geometrical aspects remaining the same, a built in beam is considered stronger than a simply supported beam . As built in beams are statically indeterminate, techniques such as linear superposition are often used to solve problems associated with them. The bending moment for a loaded built in beam is normally maximum at the end joints.

In this section we look at the Moment-Area method, and the Macaulay method (calculus method) to calculate the fixing moments and the end reaction.

Moment-area Method For Built In Beams

It follows from the Moment-Area method (See Bending of Beams Part 3) that since the change of slope from end to end and the intercept $\inline z$ are both zero, then:

$\sum A=0}$

(2)

and,

$\sum{A \bar{x}}=0$

(3)

MISSING IMAGE!

23287/Beams-I-1a.png cannot be found in /users/23287/Beams-I-1a.png. Please contact the submission author.

It is easier to consider the Bending Moment diagram for the Built in Beam in the diagram as the algebraic sum of two parts. The first considers the beam to be Simply Supported (b), and the second, due to the end moments which must be introduced to bring the slopes back to zero (c). The area and end reactions obtained, if freely supported, will be referred to as The Free Moment Diagram and the Free reactions $\inline A_1$ , $\inline R_1$ and $\inline R_2$ .

The Fixing Moments at the ends are $\inline \displaystyle M_a$ and $\inline M_b$ and in order to maintain equilibrium when $\inline \displaystyle M_a$ and $\inline M_b$ are unequal, the reactions $\inline \displaystyle R = \frac{(M_a - M_b)}{l}$ are introduced. These are upwards on the left-hand end and downwards on the right.

Due to $\inline \displaystyle M_a$ , $\inline M_b$ and $\inline R$ the Bending Moment at a distance $\inline x$ from the left-hand end is given by:

$M_x\;= - M_a + R\;x\;= - M_a + \left\{\frac{M_a - M_b}{l} \right\}\;x$

This gives a straight line going from a value of $\inline \displaystyle - M_a$ at $\inline x = 0$ to $\inline - M_b$ at $\inline x = l$ . From this can be drawn the Fixing Moment Diagram $\inline \displaystyle A_2$ (See d).

For the downward loads $\inline \displaystyle A_1$ is a positive area (Sagging $\inline BM$ ) and $\inline \displaystyle A_2$ is a negative area (Hogging $\inline BM$ ). Consequently, equations (2) and (3) reduce to:

$A_1 = A_2$

And $\inline A_1\;\bar{a}_1 = A_2 \;\bar{a}_2$ (Numerically)

These give rise to two important statements:-

Area of the Free Moment Diagram = Area of the Fixing Moment Diagram.
The Moments of Areas of Free and Fixing Diagrams are equal.

It may be necessary to break down the areas still further to obtain convenient triangles and parabolas.

These two equations allow $\inline \displaystyle M_a$ and $\inline M_b$ to be found and the total reactions at the ends are :

$\inline R_a = R_1 + R = R_1 + \displaystyle\frac{M_a - M_b}{l}$

And $\inline \;\;\;\;\;R_b = R_2 - R = R_2 - \displaystyle\frac{M_a - M_b}{l}$

The Combined Bending Moment Diagram (e) is the Algebraic sum of the two components.

Example:

[imperial]

Example - Example 1

Problem

Obtain expressions for the Maximum Bending Moment and deflection of a beam of length $l$ and a flexural rigidity $EI$ . The Beam is fixed horizontally at both ends ( built in) and carries a load $W$ which is:

a) Concentrated at mid-span.
b) Uniformly distributed over the whole beam.

Workings

a) Concentrated Load

The Fixing Moment at both ends are equal and the area of the diagram is therefore $M\;l = A_2$

The free Moment diagram is a triangle with a maximum ordinate of $\displaystyle \frac{W\;l}{4}$

$\displaystyle \therefore\;\;\;\;\;\;\;A_1 = \frac{1}{2}\;\left( \frac{W\;l}{4}\right)\;l = \frac{W\;l^2}{8}$

From Equation (1) $\displaystyle A_1 = A_2$

$\therefore\;\;\;\;\;\;M = \frac{W\;l}{8}$

Thus the combined Bending Moment diagram is as shown in the lower diagram. The Maximum Bending Moment is $\displaystyle M = \frac{W\;l}{8}$ and occurs at the ends (Hogging) and the Centre (Sagging).

By taking Moment-Areas about one end for half the beam, the intercept gives the deflection as:

$y = \frac{[\displaystyle\frac{1}{2}\left(\displaystyle\frac{W\;l}{4} \right)\left(\displaystyle\frac{l}{2} \right)]^{\frac{2}{3}} - M\left(\displaystyle\frac{l}{2} \right)\displaystyle\frac{l}{4}}{E\;I}= \frac{W\;l^3}{192\;E\;I}$

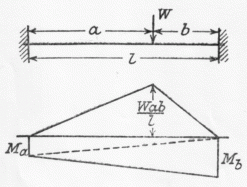
b) Uniform Load

This time the Free Moment diagram is a parabola and the area is given by:

$A_1 = \frac{2}{3}\;\left(\frac{w\;l^2}{8} \right)l = \frac{w\;l^3}{8}$

The Area of the Fixing Moment diagram $\displaystyle A_2$ is $M\;l$

Equating the areas of the Free and Fixing Moment diagrams gives $M = \displaystyle\frac{w\;l^2}{12}$

This is the Maximum Bending Moment.

As before the intercept about one end gives the deflection

i.e.

$y = \frac{[\displaystyle\frac{2}{3}\left(\displaystyle\frac{w\;l^2}{8} \right)\left(\displaystyle\frac{l}{2} \right)]^{\frac{5}{8}}\times \displaystyle\frac{l}{2}}{E\;I}= \frac{w\;l^4}{384\;E\;I}$

Note: In comparing this equation with that shown in "Bending of Beams" Appendix 3 it must be remembered that $w$ is the weight per unit length and that $W$ is the total weight. i.e. $\displaystyle W = w\;l$

Solution

a) $y = \displaystyle\frac{[\displaystyle\frac{1}{2}\left(\displaystyle\frac{W\;l}{4} \right)\left(\displaystyle\frac{l}{2} \right)]^{\frac{2}{3}} - M\left(\displaystyle\frac{l}{2} \right)\displaystyle\frac{l}{4}}{E\;I}= \frac{W\;l^3}{192\;E\;I}$
b) $y = \displaystyle\frac{[\displaystyle\frac{2}{3}\left(\displaystyle\frac{w\;l^2}{8} \right)\left(\displaystyle\frac{l}{2} \right)]^{\frac{5}{8}}\times \displaystyle\frac{l}{2}}{E\;I}= \frac{w\;l^4}{384\;E\;I}$

Macaulay Method

When the Bending Moment diagram does not lend itself to simplification into convenient areas, it may be quicker to use the calculus method (See Bending of Beams Part 3). This also has the advantage of giving the Fixing Moments and end Reactions directly, and enables the maximum deflection to be found.

Example:

[imperial]

Example - Example 1

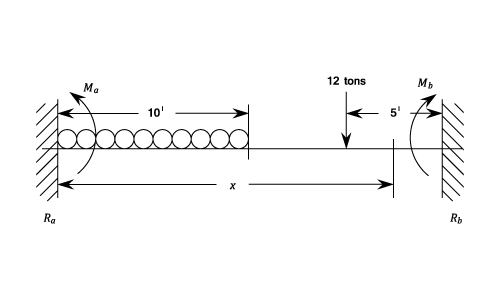
Problem

A Beam of uniform Section is built in at each end and has a span of 20 ft. It carries a uniformly distributed load of $\displaystyle\frac{3}{4} ton/ft$ on the left hand half together with a 12 ton load at 25 ft. from the left hand end.

Find the end reactions and Fixing Moments and the magnitude and position of the maximum deflection.

Workings

$E = 30\times 10^6lbs.in^{-2}$ and $I = 500in.^4$

Taking the Origin at the left hand end and let the Fixing Moments be $\displaystyle M_a$ and $M_b$ . The Reactions $\displaystyle R_a$ and $R_b$ .

Then

$E\;I\;\frac{d^2y}{dx^2}\;= - M_a + R_ax - \frac{3}{4}\times \frac{x^2}{2} + \frac{3}{4}\frac{(x - 10)^2}{2} - 12(x - 15)$

Integrating,

$E\;I\;\frac{dy}{dx}\;= - M_ax + R_a\frac{x^2}{2} - \frac{x^3}{8} + \frac{(x - 10)^3}{8} - 6(x - 15)^2 + A$

When $x = 0$ $\displaystyle\frac{dy}{dx} = 0$ $\;\therefore\;A = 0$

Integrating,

$E\;I\;y\;= - M_a\frac{x^2}{2} + R_a\frac{x^3}{6} - \frac{x^4}{32} + \frac{(x - 10)^4}{8} - 2(x - 15) + B$

When $x = 0$ $y = 0$ $\;\therefore B = 0$

Also when $x = 20$ $\displaystyle\frac{dy}{dx} = 0$ and $y = 0$

$\therefore\;\;\; - M_a\times20 + R_a\times \frac{20^2}{2} - \frac{20^3}{8} + \frac{10^3}{8}\;-6\times 5^2 = 0$

$\therefore\;\;\;\;\;\;10\;R_a - M_a = \frac{205}{4}$

(1)

$\therefore\;\;\; - M_a\times\frac{20^2}{2} + R_a\times \frac{20^3}{6} - \frac{20^4}{32} + \frac{10^4}{32}\;-2\times 5^3 = 0$

$\therefore\;\;\;\;\;\;\frac{20}{3}\;R_a - M_a = \frac{395}{16}$

(2)

Subtracting equation (2) from (1)

$\frac{10}{3}R_a = \frac{425}{16}$

Thus, $R_a = 7.97\;tons$

From equation (1)

$M_a = 28.45\;tons-ft.$

But $R_a + R_b$ = Total downwards Load = $19.5\;tons$

$\therefore\;\;\;\;\;\;R_b = 11.53\;tons$

And $- M_b$ = Value of $B.M.$ at $x = 20$

$= - 28.45 + 7.97\times 20 - \frac{3\times 20^2}{8} + \frac{3\times 10^2}{8} - 12\times 5 = -41.55\;tons-ft.$

Since the concentrated load is greater than the total concentrated load and acts at an equal distance from the nearest end, it may be deduced that zero slope occurs at a value between 10 and 15 ft.

$\therefore\;\;\;\;\;E\;I\;\frac{dy}{dx}\;= - 28.45x + 7.97\times20 - \frac{x^3}{8} + \frac{(x - 10)^3}{8} = 0$

$x^2(3.98 - 3.75) - x(28.75 - 37.5) - 125 = 0$

$0.235x^2 + 9.05x - 125 = 0$

Solving this quadratic gives:

$x = 10.8\;ft.$

Substituting this value in the deflection equation gives:-

$E\;I\;y\;= - \frac{28.45\times10.8^2}{2} + \frac{7.97\times10.8^3}{6} - \frac{10.8^4}{32} + 0.8^432\;= - 414\;tons-ft.$

Thus the maximum deflection is given by:

$\hat{y} = \frac{414\times 12^3}{13200\times 500} = 0.109\;in.$