Engineering › Fluid Mechanics › Fluid Masses ›

Accelerated along inclined plane

Fluid masses subjected to acceleration along inclined plane

View version details

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\inline \tau$ ) = $\inline I\omega\Omega$ (In the limit).

$\inline I$ = Moment of Inertia.
$\inline \omega$ = Angular velocity
$\inline \Omega$ = Angular velocity of precession.

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, writer and Catholic philosopher.

Leonhard Euler (1707-1783) was a pioneering Swiss mathematician and physicist.

Henry Philibert Gaspard Darcy (1803-1858) was a French engineer who made several important contributions to hydraulics.

Overview

Consider a tank open at top, containing a liquid and moving upwards along inclined plane with a uniform acceleration as shown in fig-1(a).

MISSING IMAGE!

23547/fluid_masses_subjected_to_acceleration_along_inclined_plane.png cannot be found in /users/23547/fluid_masses_subjected_to_acceleration_along_inclined_plane.png. Please contact the submission author.

We know that when the tank starts moving, the liquid surface falls down on the front side and rises up on the back side of the tank as shown in fig-1(b).

Let,

$\inline \phi$ = Inclination of the plane with the horizontal
$\inline \theta$ = Angle, which the liquid surface makes with the horizontal, and
$\inline a$ = Acceleration of the tank

MISSING IMAGE!

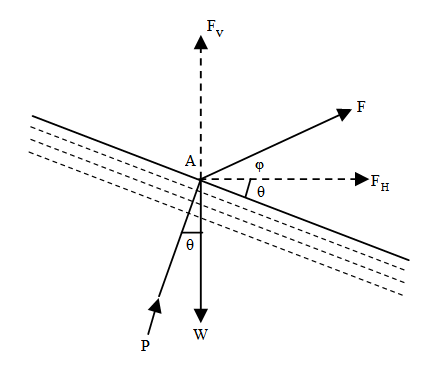
23547/fluid_inclined.png cannot be found in /users/23547/fluid_inclined.png. Please contact the submission author.

Now consider any particle A on the liquid surface. We know that the forces acting on the liquid particle are :

1. Weight of the particle (W) acting vertically down.

2. Accelerating force (F) on an angle $\inline \phi$ with the horizontal.

3. Pressure (P) exerted by the liquid particles normal to the free surface.

Now resolving the accelerating force (F) horizontally and vertically, we get

$F_H = F \cos\phi$

and

$F_V = F \sin\phi$

We know that the weight of the particle,

$W = mg$

Similarly, the accelerating force,

$F = ma$

Now resolving all the forces horizontally at A,

$P\sin\theta = F_H = F\cos\phi = ma\cos\phi$

$\Rightarrow P\sin\theta = ma\cos\phi$

(2)

And resolving all the forces vertically at A,

$P\cos\theta = F_V = F\sin\phi + W = ma\sin\phi + mg$

$\Rightarrow P\cos\theta = ma\sin\phi + mg$

(3)

Dividing equation (2) by (3)

$\frac{P\sin\theta}{P\cos\theta} = \frac{ma\cos\phi}{ma\sin\phi + mg} = \frac{a\cos\phi}{a\sin\phi + g}$

$\tan\theta = \frac{a_H}{a_V + g}$

where,

a_H = horizontal component of the acceleration
a_V = vertical component of the acceleration

Example:

[metric]

Example - Fluid masses subjected to acceleration along inclined plane

Problem

A rectangular box containing water is accelerated at 3m/s² upwards on an inclined plane 30 degree to the horizontal. Find the slope of the free liquid surface.

Workings

Given,