Login
Accelerated vertically
Fluid masses subjected to vertical acceleration
Contents
Overview
Consider a tank open at top, containing a liquid and moving vertically upwards with a uniform acceleration. Since the tank is subjected to an acceleration in the vertical direction only, therefore the liquid surface will remain horizontal.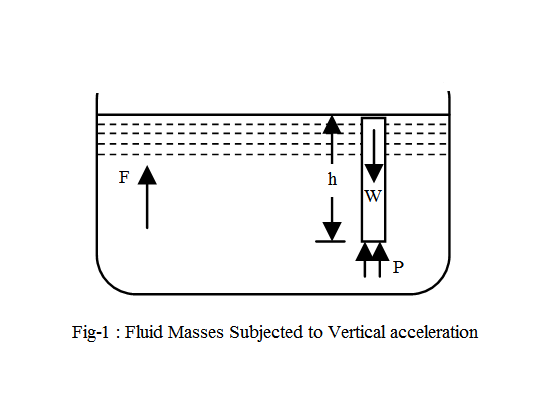
Example:
[metric]
Example - Fluid masses subjected to vertical acceleration
Problem
An open rectangular tank 4m long and 2.5m wide contains an oil of specific gravity 0.85 up to a depth of 1.5m. Determine the total pressure on the bottom of the tank, when the tank is moving with an acceleration of of g/2 m/s2 (i) vertically upwards (ii) vertically downwards.
Workings
Given,
Intensity of pressure at the bottom of the tank,
)
)
Total pressure on the bottom of the tank,
&space;=&space;187.65\;KN)
(i) Total pressure on the bottom of the tank, when it is vertically downwards
Intensity of pressure at the bottom of the tank,
)
)
Total pressure on the bottom of the tank,
&space;=&space;62.55\;KN)
= 4 m
= 2.5 m
= 1.5 m
= g/2 m/s2
- Specific gravity of liquid = 0.85