Hyperbola

Analysis of the Hyperbola

View other versions (2)

Contents

Definition
The Tangent And Normal To The Hyperbola At A Given Point
The Equation Of The Normal
The Points Of Intersection Of A Straight Line And A Hyperbola
The Director Circle
The Parametric Equations To A Hyperbola
The Parametric Equation Of A Tangent To The Hyperbola
The Normal To The Curve
The Asymptotes Of A Hyperbola
The Rectangular Hyperbola
Parametric Equation Of The Tangent
Page Comments

Definition

A hyperbola is a conic section defined as the locus of all points $\inline P$ in the plane such as the difference of whose distances from two fixed points $\inline F_1$ , $\inline F_2$ (foci) is a given positive constant $\inline k$ and $\inline F_1F_2=2c$

Workings On A Hyperbola

As with the ellipse the focus $\inline S$ is at the point $\inline (-ae,0)$ and the directrix $\inline AB$ is the line $\inline \displaystyle x = - \frac{a}{e}$ .
Since the eccentricity $\inline e$ is greater than one, the relative positions of the focus $\inline S$ and the point of intersection $\inline C$ of $\inline AB$ on the $\inline x$ axis are unchanged. However in this case $\inline C$ is nearer to the origin than $\inline S$ .

MISSING IMAGE!

22109/hyp_3.gif cannot be found in /users/22109/hyp_3.gif. Please contact the submission author.

The coordinates for the foci points are

$F_1(-\sqrt{a^2+b^2},0)$

$F_2(\sqrt{a^2+b^2},0)$

The eccentricity of a hyperbola is :

$e=\sqrt{\frac{b^2}{a^2}+1}$

If $\inline P$ is the point $\inline (x,y)$ on the curve, $\inline PM$ is the sum of the abscissa of $\inline P$ and the length $\inline CO$ . ie:

$PM = x + \frac{a}{e}$

The length $\inline PS$ is given by the equation:

$PS^2 = (x + ae)^2 + y^2$

From the definition of a Hyperbola, $\inline P$ is a point such that $\inline PS = e*PM$

$(x + ae)^2 + y^2 = e^2\;\left(x + \frac{a}{e} \right)^2$

This can be re-written as:

$(e^2 - 1)\,x^2 - y^2 = a^2\,(e^2 - 1)$

$\inline (\pm\, a,\,0)$ and $\inline y$ and it is therefore symmetrical about both axes. From this symmetry it can be deduced that there is a second Focus $\inline S'$ at the point $\inline (ae,0)$ and a second Directrix $\inline A'B'$ along the line $\inline x = \frac{a}{e}$ .The curve cuts the x-axis where $\inline \frac{x^2}{a^2} = 1$ . i.e. at the points $\inline (\pm\, a,\,0)$ shown as $\inline H$ and $\inline H'$ in the diagram. By writing $\inline x = 0$ in the equation of the curve it can be seen that the points where the curve cuts the $\inline y$ axis are given by $\inline \frac{y^2}{b^2}\;= - 1$ . As there is no real solution to this equation the points are imaginary. By writing the equation in the form:

$\frac{y^2}{b^2} = \frac{x^2}{a^2} - 1$

It is clear that $\inline y^2$ is negative and therefore there is no part of the curve for values of $\inline x$ which lie between $\inline x = a$ and $\inline x = -a$ .
On the other hand the equation can be written as:

$\frac{x^2}{a^2} = 1 + \frac{y^2}{b^2}$

Showing that points exist on the curve for all values of $\inline y$ . The above forms of the equation of a Hyperbola also show that that $\inline y$ increases as $\inline x$ increases and vice versa. The curve consists of two portions one of which extends along the $\inline x$ axis to an infinite value whilst the other extends on the negative side of the $\inline y$ axis in a similar manner.

The points $\inline H$ and $\inline H'$ are called the vertices and the line $\inline HH'$ the transverse axis of the hyperbola. The origin $\inline O$ is the centre and the chords through the origin are called diameters . The double ordinate $\inline LSL'$ through the focus is the latus-rectum and there is a second latus-rectum through the second focus $\inline S'$ . $\inline LS$ is the value of $\inline y$ when $\inline x = - ae$ . So from the equation of the hyperbola:

$LS = b\left(\frac{a^2e^2}{a^2} - 1\right)$

$\frac{1}{2} = b\;\sqrt{(\;e^2 - 1)} = \frac{b^2}{a}$

So the length of the Latus rectum $\inline \displaystyle = 2\;\frac{b^2}{a}$

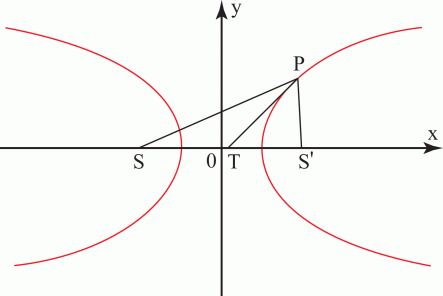
Example:

Example - Traverse axis

Problem

Show that the differences of any point on a hyperbola is equal to the length of the transverse axis.

Workings

With reference to the diagram and the equation of a hyperbola. If $x$ is the abscissa of P :

$PS = e\;PM = e\left(x + \frac{a}{e} \right) = ex + a$

Similarly if $PM'$ is drawn perpendicular to the second Directrix $A'B'$

$PS' = e\;PM' = e\left(x - \frac{a}{e} \right) = ex - a$

Solution

The differences of the focal distances $PS$ and $PS'$ is therefore equal to $2a$ , the length of the transverse axis.

The Tangent And Normal To The Hyperbola At A Given Point

The cartesian equation for a hyperbola is

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Differentiating the equation of a Hyperbola with respect to $\inline x$ :

$\frac{2x}{a^2} - \frac{2y}{b^2}\frac{dy}{dx} = 0$

So the gradient of the hyperbola at a given point $\inline (x_1,y_1)$ is given by:

$\left(\frac{dy}{dx} \right)_{x=x_1} = \frac{b^2\,x_1}{a^2\,y_1}$

The tangent at this point has the same gradient as the curve. Therefore its equation is:

$\inline \displaystyle y - y_1 = \frac{b^2\,x_1}{a^2\,y_1}(x - x_1)$ or $\inline \displaystyle b^2\,xx_1 - a^2\,yy_1 = b^2\,x_1^2 - a^2\,y_1^2$

By dividing through by $\inline a^2\;b^2$ and by using the following relationship which is a condition that the point $\inline (x_1,y_1)$ will lie on the parabola:

$\frac{x_1^2}{a^2} - \frac{y_1^2}{b^2} = 1$

A tangent line to a hyperbola is a line which intersects the curve in only one point.

The equation of the tangent can be written as :

$\mathbf{\frac{xx_1}{a^2} - \frac{yy_1}{b^2} = 1}$

The Equation Of The Normal

The slope or gradient of a line describes incline, or grade.

Given $\inline A(x_1,y_1)$ and $\inline B(x_2,y_2)$ the slope for the line $\inline (AB)$ is
$\inline \displaystyle m=\frac{y_2-y_1}{x_2-x_1}$ .

The normal at the point $\inline (x_1,y_1)$ is the line through this point perpendicular to the tangent.
Its slope is therefore given by: $\inline \displaystyle -\frac{a^2\,y_1}{b^2\,x_1}$

And its equation is:

$\mathbf{y - y_1 = \frac{a^2\,y_1}{b^2\,x_1}(x - x_1)}$

Example:

Example - Tangent and normal

Problem

Write down the equation of the tangent and normal at the point $(4,\,3\sqrt{3})$ to the Hyperbola:

$9x^2 - 4y^2 = 36$

Workings

The equation of the Hyperbola can be written in the form:

$\frac{x^2}{4} - \frac{y^2}{9} = 1$

Solution

So the equation of the tangent at the required point is :

$\frac{4x}{4} - \frac{3\,\sqrt{3}\;y}{9} = 1\;\;\;\;or\;\;\;\;3x\;-\sqrt{3}\;y = 3$

And the equation of the Normal at the same point is :

$\frac{x - 4}{\frac{4}{4}} = \frac{y - 3\sqrt{3}}{\frac{3\sqrt{3}}{(-9)}}}$

$x + 3\sqrt{3}y = 13$

The Points Of Intersection Of A Straight Line And A Hyperbola

As the equation of a hyperbola only differs from that of an ellipse by having $\inline - b^2$ instead of $\inline b^2$ many of the results derived for the ellipse apply to the Hyperbola provided that the sign of $\inline b^2$ is changed.

The analysis of of the points of intersection of the line $\inline y = mx + c$ with an ellipse applies if the sign of $\inline b^2$ is changed through out. It is found that the line meets the Hyperbola in real, coincident or imaginary points depending upon whether $\inline c^2$ is equal, greater or less than $\inline a^2m^2 - b^2$ .

It can also be found that the following line always touches the Hyperbola:

$y = mx + \sqrt{(a^2m^2 - b^2)}$

The Director Circle

Using the same substitution as above it can be found that the locus of the points of intersection of perpendicular tangents to the hyperbola is the circle;

$x^2 + y^2 = a^2 - b^2$

This circle is called the director circle. It should be noticed that whereas for an ellipse $\inline b<a$ there is no such limitation in the case of a hyperbola. The radius of the director circle being $\inline \sqrt{(a^2 - b^2)}$ , the circle is real whenever $\inline \sqrt{(a^2 - b^2)}$ $\inline b^2\;<\;a^2.\;\;If\;b^2 = a^2$ , the radius of the circle is zero and it reduces to a point circle at the origin and in this case the centre of the hyperbola is the only point from which perpendicular tangents can be drawn to the curve. If $\inline b^2\;>\;a^2$ , the radius of the director circle is imaginary and no perpendicular tangents can be drawn to the hyperbola.

The Parametric Equations To A Hyperbola

An ordinate of the Hyperbola does not meet the auxiliary circle on $\inline HH'$ as diameter in real points. There is thus no real eccentric angle as in the case of the ellipse. However it is often useful to be able to express the coordinates of any point on the circle in terms of one variable.

Since $\inline sec^2\,\theta = 1 + tan^2\,\theta$ , the equations:

$x = a\;sec\,\theta\;\; ,\;\;\;y = b\;tan\,\theta$

may be used for these expressions clearly satisfy the equation of the hyperbola:

$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$

Whilst it is possible to give a geometrical definition of the angle $\inline \theta$ ,there is little value in so doing. However parametric equations can be very useful in some solutions.

The Parametric Equation Of A Tangent To The Hyperbola

Using the parametric coordinates of a point:

$\frac{dx}{d\theta } = a\;sec\,\theta \;tan\,\theta \;\;\;\;,\;\;\;\;\frac{dy}{d\theta } = b\;sec^2\,\theta$

So the gradient of the Hyperbola at the point $\inline (a\;sec\,\theta\,,\;b\;tan\,\theta)$ is given by:

$\frac{dy}{dx} = \frac{dy}{d\theta }\times\frac{d\theta }{dx} = \frac{b\;sec^2\,\theta }{a\;sec\,\theta \;tan\,\theta } = \frac{b\;sec\,\theta }{a\;tan\,\theta }$

The equation of tangent at the point is therefore given by:

$y - b\;tan\,\theta = \frac{b\;sec\,\theta }{a\;tan\,\theta }(x - a\;sec\,\theta )$

Which simplifies to :

$\mathbf{\frac{x}{a}\;sec\,\theta - \frac{y}{b}\;tan\,\theta = 1}$

The Normal To The Curve

The normal is the line which passes through the point $\inline (a\;sec\,\theta\,\;b\;tan\,\theta)$ with slope $\inline \displaystyle -\frac{b\,sec\,\theta }{a\;tan\,\theta }$

The equation is therefore:

$y - b\;tan\,\theta\;= - \frac{a\;tan\,\theta }{b\;sec\,\theta }(x - a\;sec\,\theta )$

The equation of the Normal is therefore:

$\mathbf{ax\;sin\,\theta + by = (a^2 + b^2)tan\,\theta}$

Example:

Example - Inclined foci

Problem

If $S$ , $S'$ are the foci and $P$ is any point on a hyperbola, show that $SP$ , $S'P$ are equally inclined to the tangent at $P$ .

Workings

$S$ is the focus $(-ae,0)$ and $S'$ the focus $(ae,0)$ of the hyperbola.

$P$ is the point $(a\;sec\,\theta ,b\;tan\,\theta)$ and the tangent at $P$ cuts the x-axis at the point $T$ . The equation of the tangent at $P$ is :

$\frac{x\;sec\,\theta }{a} - \frac{y\;tan\,\theta }{b} = 1$

The abscissa of $T$ is found by putting $y = 0$ into this equation. The abscissa of $T$ is therefore given by:

$x = \frac{a}{sec\,\theta } = a\,cos\,\theta$

hence

$ST = ae + a\;cos\,\theta \;\;\;\;and\;\;\;\;S'T = ae - a\,cos\,\theta$

therefore

$\frac{ST}{S'T} = \frac{ae + a\;cos\,\theta }{ae - a\;cos\,\theta } = \frac{e + cos\,\theta }{e - cos\,\theta }$

But it has already been shown in a previous example (Equation) that if $x$ is the abscissa of $P$ then $PS = ex + a$ and $PS' = ex - a$ . In this example $x\.=\.s\;sec\,\theta$ .

$\frac{PS}{PS'} = \frac{ae\,sec\,\theta + a}{ae\,sec\,\theta - a} = \frac{e + cos\,\theta }{e - cos\,\theta }$

therefore

$\frac{ST}{S'T} = \frac{PS}{PS'}$

Area of triangle $PTS' = \frac{S'T\times h}{2}$ Area of triangle $PTS = \frac{ST\times h}{2}$

But using the sine rule on the two triangles:

Area of triangle $PTS = \frac{PS\times PT\;sin\,\theta }{2}$

Area of triangle $PTS' = \frac{PS'\times PT\;sin\,\phi }{2}$

$\frac{Area\;of\;triangle\;PTS }{Area\'of\;triangle\;PS'T} = \frac{PS\;sin\,\theta }{PS'\;sin\,\phi } = \frac{ST}{S'T}$

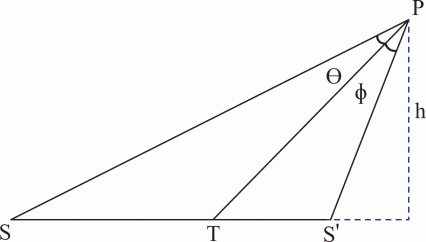
Solution

Thus provided that $\theta = \phi$ the conditions necessary are met and $PT$ bisects the angle $SPS'$

The Asymptotes Of A Hyperbola

Lines which meet a hyperbola at two points both of which are situated at an infinite distance but which are not themselves altogether at infinity are called asymptotes

The abscissa of the points of intersection of the straight line and a hyperbola ca be found by writing the equation of the line into the standard equation of the curve. This gives:

$\frac{x^2}{a^2} - \frac{(mx + c)^2}{b^2} = 1$

This can be re-written as a quadratic in $\inline \displasystyle \frac{1}{x}$ . Hence:

$\frac{a^2(c^2 + b^2)}{x^2} + \frac{2a^2mc}{x} + a^2m^2 - b^2 = 0$

If $\inline a^2m^2 - b^2\;and\;a^2mc$ are both zero this equation in $\inline \displaystyle \frac{1}{x}$ has two zero roots. In other words if :

$m = \pm \frac{b}{a};c = 0$

The line $\inline y = mx + c$ meets Hyperbola in two points at each of which $\inline 1/x$ is zero. i e the line meets the Hyperbola at two points situated at an infinite distance from the centre of the curve.

$y = \pm \frac{b}{a}\;x$

The asymptotes of the hyperbola are therefore the lines:

$y = \pm \frac{b}{a}\;x$

These two lines pass through the centre of the Hyperbola (The origin) and are equally inclined to the x-axis. Written as a single equation the Asymptotes are given by :

$\left(y - \frac{b}{a}\;x \right)\;\;\left(y + \frac{b}{a}\;x \right)\/=\/0$

MISSING IMAGE!

22109/hyp_4.gif cannot be found in /users/22109/hyp_4.gif. Please contact the submission author.

The above equation can be re-written as:-

$\frac{y^2}{b^2} - \frac{x^2}{a^2} = 0$

The Rectangular Hyperbola

The equation of a Hyperbola is :

$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$

$\inline a = b$ then the equation of the Asymptotes is $\inline \;y = \pm\,x$ . The asymptotes are therefore inclined at an angle of $\inline \pm\,45^0$ to the x-axis.
The equation of this curve known as the Rectangular Hyperbola is :

$x^2 - y^2 = a^2$

The Equation Of A Rectangular Hyperbola Referred To Its Asymptotes

The equation of a Rectangular Hyperbola takes a very simple form when the axes of the coordinates coincide with the Asymptotes.

MISSING IMAGE!

22109/hyp_5.gif cannot be found in /users/22109/hyp_5.gif. Please contact the submission author.

If in the above diagram $\inline P$ is a point on the curve and the coordinates of $\inline P$ are $\inline (X,Y)$ are measured from the lines $\inline OX$ . $\inline OY$ bisecting the angles between the two asymptotes $\inline Ox$ , $\inline Oy$ , $\inline X$ and $\inline Y$ are related by

$X^2 - Y^2 = a^2$

$\inline PK$ , $\inline PM$ are drawn perpendicular to $\inline OX$ , $\inline Ox$ respectively and $\inline ML$ , $\inline MN$ are drawn perpendicular to $\inline PK$ , $\inline OX$ as shown. Since the angle $\inline XOx$ is $\inline 45$ degrees

$OK = NK + ON = ML + ON$

$= PM\,cos\,45^0 + OM\,cos\,45^0 = \frac{PM + OM}{\sqrt{2}}$

And

$PK = PL - KL = PL - MN$

$= PM\,sin\,45^0 - OM\,sin45^0 = \frac{PM - OM}{\sqrt{2}}$

If $\inline Ox$ , $\inline Oy$ are taken as the coordinate axes, $\inline OM = x$ , $\inline PM = y$ and since $\inline OK = X$ , $\inline PK = Y$ the above result gives :

$X = \frac{y + x}{\sqrt{2}},\;Y = \frac{y - x}{\sqrt{2}}$

Substituting in equation (56)

$\frac{(y + x)^2}{2} - \frac{(y - x)^2}{2} = a^2$

$xy = \frac{a^2}{2}$

Writing $\inline 2c^2 = a^2$ the equation takes the very simple form of :

$xy = c^2$

When a rectangular hyperbola is referred to its asymptotes as axes a point whose coordinates are given by :

$x = ct,\;y = \frac{c}{t}$

always lies on the curve as these coordinates satisfy the equation $\inline x\,y = c^2$ .

The equations $\inline x = ct$ and $\inline y = c/t$ give a parametric representation of a Rectangular Hyperbola and the point given by them may be called the point " $\inline t$ ". Thus

$6\sqrt{3}\;t^2 + 7t\;-8\sqrt{3} = 0$

Parametric Equation Of The Tangent

If we differentiate the equations with respect to $\inline t$ we get:

$\frac{dx}{dt} = c\,,\;\frac{dy}{dt}\;= - \frac{c}{t^2}$

and the gradient of the Rectangular Hyperbola $\inline xy = c^2$ at the point "t" is given by;

$\frac{dy}{dx} = \frac{dy/dt}{dx/dt}\;= - \frac{c/t^2}{c}\;= - \frac{1}{t^2}$

The tangent at this point is therefore the line:

$y - \frac{c}{t}\;= - \frac{1}{y^2}(x - ct)$

$\mathbf{x + t^2y = 2ct}$

Example:

Example - Equation of the normal

Problem

Find the equation of the normal at the point $(3,4)$ to the Rectangular Hyperbola $xy = 12$ and the coordinates of its second point of intersection with the curve.

In this example $c^2 = 12\;\;\;\;\;and\;so\;\;\;\;c = 2\sqrt{3}$ . The parameter $t$ of the point $(3,4)$ is given by :

$3=2\sqrt{3}t$

Workings

The equation of the normal is given by:

$\left(\frac{\sqrt{3}}{2} \right)^2x - y = 2\sqrt{3}\left[\left(\frac{\sqrt{3}}{2} \right)^2 - \frac{2}{\sqrt{3}} \right]$

$3x - 4y + 7 = 0$

Let the second point of intersection of the Normal be the point $(2\sqrt{3}t,\;\frac{2\sqrt{3}}{t})$ and since this point lies on the line $3x - 4y + 7 = 0$

$6\sqrt{3}t - \frac{8\sqrt{3}}{t} + 7 = 0$

This can be written in the form ;

$(2t - \sqrt{3})(3\sqrt{3}\;t + 8) = 0$

Solution

From this it can be seen that :

$t = \frac{1}{2}\sqrt{3}\;\;\;\;or\;\;\; - \frac{8}{3\sqrt{3}}$

The first value of $t$ corresponds to the point $(3,4)$ and so the coordinate of the second point of intersection by using second value. With this value for $t$ the point

$\left( 2\sqrt{3}\;t, \frac{2\sqrt{3}}{t} \right)\;\;\;\;becomes\;the\;point\;\left(- \frac{16}{3},- \frac{9}{4}} \right)$