Engineering › Fluid Mechanics › Pipes › Head Loss ›

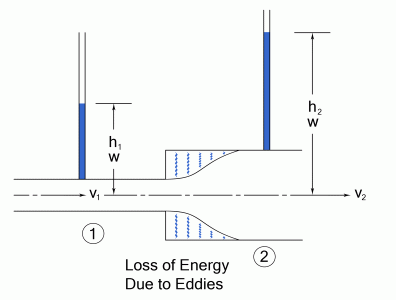
Change in Pipe Section

Pressure head loss due to change in pipe size or shape

View other versions (2)

Contents

Overview
Sudden Enlargement
Sudden Contraction
Head Loss At An Obstruction (e.g. A Valve)
Page Comments

Key Facts

Gyroscopic Couple: The rate of change of angular momentum ( $\tau$ ) = $I\omega\Omega$ (In the limit).

= Moment of Inertia.
$\omega$ = Angular velocity
$\Omega$ = Angular velocity of precession.

Overview

The sudden changes or the introduction of bends or valves disturbs the flow pattern along the pipe. The result is an increase in turbulence and this increases the frictional losses.

Sudden Enlargement

$h_l\:= \frac{(v_1\:-\:v_2)^2}{2g}$

Note: The pressure just inside the larger pipe is the same as that in the small pipe!

Momentum at section (1) = Mass $\times$ Velocity = $\frac{w}{g}\;a_1\,v_1\times \:v_1$

Momentum at section (2) = $\frac{w}{g}\:a_2\:v_2\times \;v_2$

Drop in momentum

$= \frac{w}{g}\:a_1\:v_1\,(v_1\:-\:v_2)$

for this to happen there must be a force opposing motion

The magnitude of the force = $p_2\,a_2\:-\:p_1\,a_1\:-p_1(a_2\:-\:a_1) = a_2\:(p_2\:-\:p_1)$

$\therefore\;\;\;\frac{p_2\:-\:p_1}{w} = \frac{v_2(v_1\:-\:v_2)}{g}$

Applying Bernoulli:

$\frac{p_1}{w}\:+\:\frac{v_1^2}{2g}\:= \frac{p_2}{w}\:+\:\frac{v_2^2}{2g}\:+\:h_l$

$\therefore\;\;\;\frac{v_1^2\:-\:v_2^2}{2g}\:=\:\frac{p_2\:-\:p_1}{w}\:+\:h_l$

$\therefore\;\;\;h_l = \frac{v_1^2\:-\:v_2^2}{2g}\:-\:\frac{p_2\,-\,p_1}{w}$

$\Rightarrow h_l= \frac{v_1^2\:-\:v_2^2}{2g}\:-\:\frac{v_2(v_1\:-\,v_2)}{g}$

$\therefore\;\;\;h_l\:= \frac{(v_1\:-\:v_2)^2}{2g}$

Sudden Contraction

The coefficient of Contraction is defined as :

$=\frac{a_C}{a}\f$

where a_C is the area of the choke and a is the area of the pipe
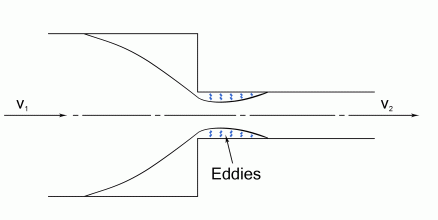
The head lost is given by:

$h_L=\frac{v^2}{2g}\left ( \frac{1}{C_C}-1 \right )^2=k\times \frac{v^2}{2g}$

(2)

k is a constant and in this case is approximately 0.5. The value of

varies with the application and a selection are shown in the table at the end of this section.

Loss of head, h_L is given by:

$h_L=\frac{(v_c\:-\:v)^2}{2g}$

But:

$a_c\:v_c\;=\:av$

And:

$v_c\:=\:\frac{v}{C_c}\:=\:\frac{a_c}{a}$

$\therefore\;\;\;h_l = \frac{1}{2g}\;\left( \frac{v}{c_0}\:-\:v \right)^2$

$=\:\left( \frac{1}{c_c}\:-1 \right)^2\;\frac{v^2}{2g}=k\times \frac{v^2}{2g}$

Head Loss At An Obstruction (e.g. A Valve)

The general equation for the head loss due to an obstruction, including bends, elbows, gate values, etc, is

$h_L=k\frac{v^2}{2g}$

where

k is the constant associated with the obstruction
v is velocity

Some typical values for k are:

Fitting or Obstruction	Value for K
Standard 45 degree Elbow	0.5
Standard 90 degree Elbow	1.0
Globe Value - fully open	10.0
Gate Valve - fully open	0.2

Proof

$h_L=\frac{(v_C-v)^2}{2g}$

$\therefore \;\;\;\;\;h_L=\frac{v^2}{2g}\left ( \frac{A}{A-a}-1 \right )^2=\frac{v^2}{2g}\left ( \frac{1}{C_C} -1\right )$

$=k\times \frac{v^2}{2g}$