Nozzles and mouthpieces
An analysis of the head lost in a nozzle and the resulting velocity of the jet.
Contents
Introduction
It is assumed that the Head H is the head behind the nozzle, and that all pipeline and valve losses have been accounted for elsewhere. There are, of course, losses in the nozzle itself, and the actual velocity of discharge will be less than the theoretical value by one to five percent. This is catered for by the use of The Coefficient of Velocity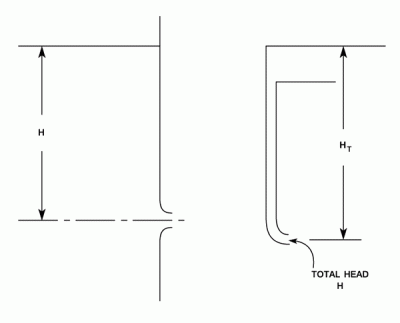
The Power Of A Jet
Example:
[imperial]
Example - Discharge through nozzle
Problem
A Nozzle discharges 175 galls per min. under a head of 200 ft. The diameter of the nozzle is 1 in. and the diameter of the jet is 0.9 in.
Find the:
- a) The coefficient of velocity for the jet.
- b) The head lost in the nozzle.
- c) The horse power available in the jet.
Workings
(a) The Coefficient of Contraction,  is given by:
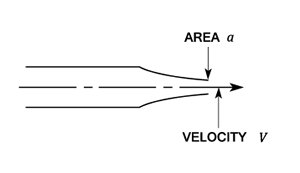
The theoretical discharge Q = The nozzle area X. From equation (#8) velocity (neglecting losses) is
therefore
Since 1 gallon of water weighs 10 lb. and 1 cubic foot of water weighs 62.4 lb, then
and the coefficient of discharge
From equation(#4), the Coefficient of velocity
(b) Using Equation (#8)
i.e.
therefore
Thus
(c) The horse power of the jet is dependent upon the weight of water per second and the head of water in the jet
Thus
is given by:
The theoretical discharge Q = The nozzle area X. From equation (#8) velocity (neglecting losses) is
therefore
Since 1 gallon of water weighs 10 lb. and 1 cubic foot of water weighs 62.4 lb, then
and the coefficient of discharge
From equation(#4), the Coefficient of velocity
(b) Using Equation (#8)
i.e.
therefore
Thus
(c) The horse power of the jet is dependent upon the weight of water per second and the head of water in the jet
Thus
Solution
a) The coefficient of velocity for the jet = 0.932
b) The head lost in the nozzle = 26.28 ft
c) The horse power available in the jet = 9.21 h.p
 Login
Login

