Air Motors
The application of the gas laws to Air Motors
Contents
Isothermal Operation
- Work Done =
It is not possible to expand the Air down to Atmospheric Pressure. By opening the valve early the small loss in work done is accompanied by a large decrease in the Swept Volume.
Work output = Area of Diagram =MISSING IMAGE!
23287/Air-Motors-0025.png cannot be found in /users/23287/Air-Motors-0025.png. Please contact the submission author.
Example:
[imperial]
Example - The application of the gas laws to Air Motors
Problem
A reciprocating Air Motor of bore 13.54 in. and Stroke 18 in. is supplied with Air at  and 90 psi. Find the Work output per cycle with complete expansion to 15 psi. Find also the percentage loss of output resulting from a decrease of stroke to 12 in. with incomplete expansion. Neglect Clearance and take the Index of expansion as 1.25.
and 90 psi. Find the Work output per cycle with complete expansion to 15 psi. Find also the percentage loss of output resulting from a decrease of stroke to 12 in. with incomplete expansion. Neglect Clearance and take the Index of expansion as 1.25.
Workings
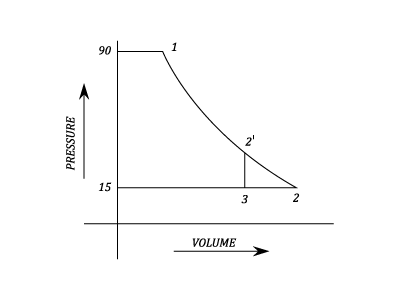
Solution
Work out put per cycle is  The loss of Power is
The loss of Power is 
 Login
Login

