Struts

An analysis of Struts using the EULER Formula.

View other versions (6)

Contents

Overview
Description
Pin Ended Strut Axially Loaded.
Direction Fixed At Both Ends
Partial Fixing Of The Ends
Direction Fixed At One End And Free At The Other
Direction Fixed At One End And Position Fixed At The Other
Strut With An Eccentric Load
Strut With Initial Curvature
Page Comments

Overview

By definition any member of a structure which is in Compression may be called a Strut. However, the term is usually reserved for long slender members which are likely to fail through buckling, rather than from compressive stress.
As a structural member resisting longitudinal compression, a strut is commonly used in architecture and engineering. In relation to engineering applications, such as for automobiles and aeronautical structures, a strut can be used as a passive brace to reinforce the body, or as an active stress bearing component. As an example, lift struts (still used today on small light aeroplanes) are commonly employed to carry both tension and compression as the aircraft maneuvers in flight.

Description

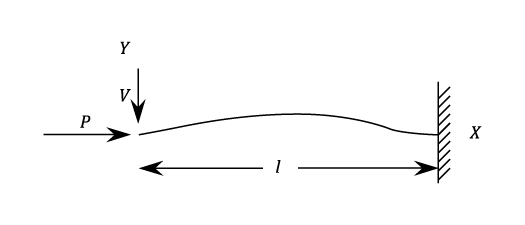
The resistance of any member to bending is determined by it's flexural rigidity EI, but

$I=Ak^2$

(1)

where, A is the cross sectional Area and k is the radius of gyration.

So for a given material, the Load per unit area which a member can withstand is related to k. There will be two principal moments of Inertia and off these the least is taken.

The Slenderness Ratio is given by :

$\frac{\text{Length of Member}}{\text{Least Radius of Gyration}}$

(2)

i.e

$\frac{l}{k}$

(3)

The value of this ratio will determine whether a member falls into the category of Struts or Columns. Struts which fail by buckling before the limiting compressive stress is reached , can be analysed by the Euler Theory.

Pin Ended Strut Axially Loaded.

It is assumed that the Strut is initially straight and that the compressive load is applied axially.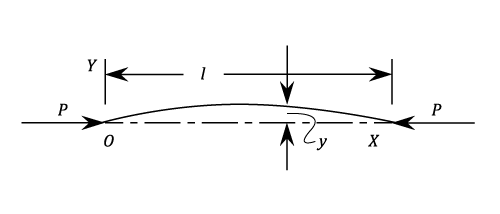

Applying the equation of bending of beams:

$EI\;\frac{D^2y}{dx^2} = M = -Py$

(4)

Substituting

$\alpha ^2 = \frac{P}{EI}$

(5)

$\frac{d^2y}{dx^2} + \alpha ^2y =0$

(6)

The Solution of which is given by:

$y = A\;sin\,\alpha x + B\;cos\,\alpha x$

(7)

when x = 0 and y = o then B = 0 when x = l and y = o then $A\;sin\;\alpha\,l = 0$

From which either A = 0 and as a result y = 0 for all values of x. In this case the strut will not buckle. Or A is indeterminate. The least value to satisfy $\sin \alpha\,l$ is $\phi$ .

This corresponds to

$\alpha ^2 = \frac{\pi ^2}{l^2} = \frac{P}{EI}$

(8)

From this it is possible to obtain the least value of P which will cause the Strut to buckle. This is called the Euler Crippling Load $P_e$ where,

$P_e = \frac{\pi ^2\,E\,I}{l^2}$

(9)

It must be stressed that the value of "I" used here is the least Moment of Inertia.

The interpretation of this analysis is that for all values of P other than those which make $\sin \alpha l=0$ , the Strut will remain perfectly straight $(y = A\;sin\;\alpha\,x = 0$ . For the particular value $P_e=\pi ^2 \frac{E\,I}{l^2} \sin \alpha \,l =0$ and $y=A \sin\frac{\pi x}{l}$ , the strut is in neutral equilibrium and theoretically any deflection which it is given, will be maintained. This is subject to the limitation that "l" remains reasonably constant and in practice any slight increase in load at the critical value will cause the deflection to increase appreciably until the material fails by yielding. Neither the Maximum stress nor the Deflection are proportional to the load.

Example:

[imperial]

Example - Maximum Deflection of a strut in a strut testing machine

Problem

A straight Alloy bar 35 inches long and with a cross section of 1/2 and 3/16 inches, is mounted in a strut testing machine. It is loaded until it buckles. Assuming that the Euler Formula applies, estimate the maximum central deflection before the material attains it's yield point of 18 Tons/in². E = 4690 Tons/in².

Workings

There will be no deflection until the Euler load is reached. This load is given by:

$Load =\frac{\pi ^2\,E\,I}{l^2}$

(1)

$= \frac{\pi ^2\times 4690\times \frac{1}{2}\times (\frac{3}{16})^2}{35^2\times 12}}$

(2)

$= 0.0104\;Tons$

(3)

The Maximum Bending Moment $\delta$ occurs at the centre where:

$\delta = \frac{0.0104}{P}$

(4)

The Maximum Stress is the sum of Direct and Bending stress at the centre.

$i.e.\;\;\;\;\;18 = \frac{0.0104}{\frac{1}{2}\times \frac{3}{16}} + \frac{0.0104\,\delta\times 6}{\frac{1}{2}\times (\frac{3}{16})^2}$

(5)

$\therefore\;\;\;\;\;\delta = \frac{17.89}{3.54} = 5.05\.ins.$

(6)

Solution

The maximum deflection $\delta$ = 5.05 $ins$

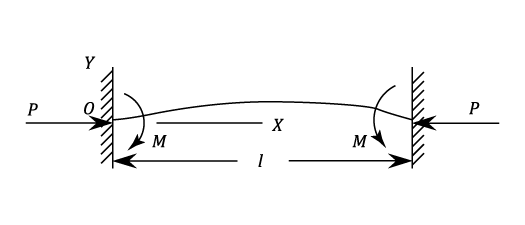
Direction Fixed At Both Ends

Assume that the Strut has deflected and that there is a bending moment at the ends.

Then,

$E\;I \frac{d^2y}{dx^2} =-P\;y+M$

(10)

Putting

$\alpha ^2 = \frac{P}{E\;I}$

(11)

Then,

$\frac{d^2y}{dx^2} + \alpha ^2y = \frac{M}{E\;I}$

(12)

$\therefore\;\;\;\;\;y = A\sin \alpha x + B \cos \alpha x + \frac{M}{E\;I \alpha^2}$

(13)

When x = 0 ; y = 0

$\therefore\;\;\;\;\;\;B\;= - \frac{M}{E\;I\;\alpha ^2}\;= - \frac{M}{P}$

(14)

And since

$\frac{dy}{dx} = 0\;\;\;\;\;A=0$

(15)

$\therefore\;\;\;\;\;y = \frac{M}{P}(1-\cos \alpha \,x)$

(16)

When x = l ; y = 0

$\alpha l = 2\times \pi$

(17)

$\therefore \text{The Buckling Load},\;P_e = 4\pi ^2\times \frac{E\;I}{l^2}$

(18)

Note. This case is equivalent to a pin-ended Strut of length $\frac{l}{2}$ . To allow for imperfect fixing it is common to allow an equivalent length of between 0.6 an 0.8 times the length l.

Partial Fixing Of The Ends

Example:

[imperial]

Example - Partial Fixing Of The Ends

Problem

A Strut of length 2a has each end fixed in an elastic material which exerts a restraining Moment $\mu$ per unit of angular displacement. Prove that the critical Load P is given by the equation $\mu\;n \tan\;na+P=0$ where $n^2=\frac{P}{E\;I}$ . Such a Strut 8ft. 4in. long has a critical load of 3,500 lbs. on the assumption that it is pin ended. Determine the percentage increase in the Critical Load is the constraints offered at the ends is 1,55 lb. in per degree of Rotation.

Workings

If M be the restraining Moment at both ends then

$y=A\sin(nx)+B\cos(nx) + \frac{M}{P}$

(7)

Using the notation given in the question.

At $x=0$ , $y=0$ and $B=-\frac{M}{P}$ And

$M=\mu\left(\frac{dy}{dx} \right)0=\mu\times A$

(8)

$\therefore\;\;\;\;\;A = \frac{M}{\mu\;n}$

(9)

Thus

$y=\left(\frac{M}{\mu\;n} \right)sin\,nx+\left(\frac{M}{P} \right)\left(1-cos\;n\,x \right)$

(10)

At the centre $x=a$ , $\frac{dy}{dx}=0$

$\therefore\;\;\;\;\;\left(\frac{M}{\mu} \right)cos\;na + \left(\frac{Mn}{P} \right)sin\;na = 0$

(11)

i.e.

$\mu\;n\;tan\;na + P =0$

(12)

For pinned ends:

$\frac{\pi ^2\;E\,I}{(2a)^2} = 3500$

(13)

$From\; which\;\;\;\;\;E\,I = 3,550,000\;lb.in^2.$

(14)

$n = \sqrt{\frac{P}{E\,I}} = \sqrt{\frac{P}{\sqrt{3,550,000}}}$

(15)

$\mu = 1500\times57.3\;lb.in./radian\;\;\;\;(given)$

(16)

Substituting in equation (37)

$tan\left(\frac{50}{1884}\sqrt{P} \right)\;= - \frac{P}{\mu\;n} = 0.0219\sqrt{P}$

(17)

The least solution of this equation is $\sqrt{p} = 79,\;\;i.e.\;P = 6230\;lbs.$ . This is an increase of 78% over the value for pin ended

Solution

This is an increase of 78% over the value for pin ended

Direction Fixed At One End And Free At The Other

This is clearly the same as a pin ended strut of length 2l

hence

$P_e=\frac{\pi ^2\;EI}{4\;l^2}$

(19)

Direction Fixed At One End And Position Fixed At The Other

Let V be the lateral force required to maintain the position of the pinnend end.

$E\;I \frac{d^2y}{dx^2} =-Py -V\,x$

(20)

If $\alpha^2=\frac{P}{E\,I}$

$\frac{d^2y}{dx^2} + \alpha^2y = -\frac{V\,x}{E\,I}$

(21)

From which,

$y = A\sin \alpha x + B \cos \alpha x - \frac{V\,x}{P}$

(22)

When x = 0 , y = 0

$B=0$

(23)

When x = l , y = 0

$A\sin\,\alpha\,l = \frac{V}{P}$

(24)

And when $\frac{dy}{dx}=0$

$A\;\alpha\times \cos \alpha\;l = \frac{V}{P}$

(25)

From which,

$\tan \alpha\;l = \alpha\;l$

(26)

$P_e = 20.2\;\frac{E\;I}{l^2} = 2.05\;\pi ^2\frac{E\;I}{l^2}$

(27)

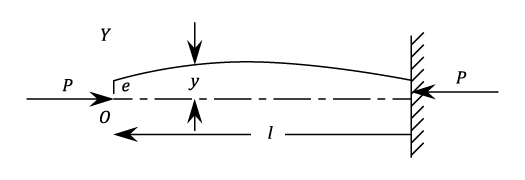
Strut With An Eccentric Load

If e is the eccentricity of the Applied Load, and the deflection y is measured from the line of action of the load ( see diagram).

Then

$E\,I\;\frac{d^2y}{dx^2}\;= - Py$

(28)

Then as before:-

$y = A \sin \alpha x + B \cos \alpha x$

(29)

When x = 0, y = e and therefore B = e When $x=\frac{l}{2}$ and $\frac{dy}{dx}=0$

$\therefore\;\;\;\;\;A \cos \frac{\alpha\;l}{2} - B\sin \frac{\alpha\;l}{2} = 0$

(30)

Thus,

$A =e \tan \frac{\alpha l}{2}$

(31)

$\therefore\;\;\;\;\;y = e \left[(tan \frac{\alpha l}{2}) \sin \alpha x+ \cos \alpha x \right]$

(32)

Note: for an eccentric load the strut will deflect for all values of P and not only for the critical Value. The deflection will become infinite for $\;tan\;\frac{\alpha\;l}{2} = Infinity\;\;\;i.e.\alpha\;l = \pi$ giving the same crippling load $\;P_e = \pi^2\;\frac{E\;I}{l^2}$ . However, due to the additional bending moment set up by the deflection, the Strut will always fail by compressive stress before the Euler Load is reached.

$y_{max} = \left[(\tan \frac{\alpha\;l}{2})(\sin \frac{\alpha\;l}{2}) + cos\frac{\alpha l}{2} \right]$

(33)

$= e \left(\frac{\sin^2 \alpha l/2 + cos^2\;\alpha\,l/2}{cos\;\alpha\,l/2} \right)$

(34)

$= e \sec\frac{\alpha\,l}{2}$

(35)

The Maximum Bending Moment is given by:-

$M_{max}=P\;y_{max}$

(36)

$= P\;e\sec\frac{\alpha\;l}{2}$

(37)

The Maximum stress

$f_{max}=\frac{P}{A}+\frac{M}{Z}$

(38)

is obtained by combing the bending and direct stress.

Strut With Initial Curvature

These are treated as a beam with an initial radius of curvature such that:-

$R_0 \approx \frac{1}{\frac{d^2y_0}{dx^2}}$

(39)

Using Equation 10 "Bending of Curved Beams"

$M = EI\left(\frac{1}{R}-\frac{1}{R_0} \right)$

(40)

Thus

$EI\;\frac{d^2y}{dx^2}=M+EI\;\frac{d^2y_0}{dx^2}$

(41)

$\therefore\;\;\;\;\;\frac{d^2y}{dx^2}+\alpha^2y=\frac{d^2y_0}{dx^2}$

(42)

Under an end load P, the initial shape of the strut $y_0$ may be assumed to be circular, parabolic or sinusoidal without making much difference to the final result. But the most convenient form is:

$y_0=c\sin \frac{\pi x}{l}$

(43)

This satisfies the end conditions and corresponds to a maximum deviation of c . Any other shape could be analysed into a Fourier series of sine terms.

Then,

$\frac{d^2y}{dx^2}+\alpha^2\;y\;=-\left(c\times\frac{\pi ^2}{l^2} \right)\left(sin\;\frac{\pi \;x}{l} \right)$

(44)

The complete solution of which is :

$y=A \sin \alpha x + B\cos \alpha x - \frac{c \pi ^2/l^2}{-\pi ^2/l^2 + \alpha^2}\times \sin \frac{\pi x}{l}$

(45)

When $x = 0$ and $y = 0$ then $B = 0$

and when $x=l/2$ and $dy/dx=0$ then $A = 0$

Hence,

$y=\frac{c \pi^2/l^2}{\pi^2/l^2 - \alpha^2}\times \sin \frac{\pi x}{l}\f] \[=\left[\frac{c\;P_e}{P_e - P} \right]\left(\sin \frac{\pi \,x}{l} \right)$

(46)

The Crippling load is $P=P_e=\frac{\pi ^2\;E\,I}{l^2}$

And

$M_{max}=P\;y_{max}=c\frac{PP_e}{(P_e-P})$

(47)

Example:

Example - Strut With Initial Curvature

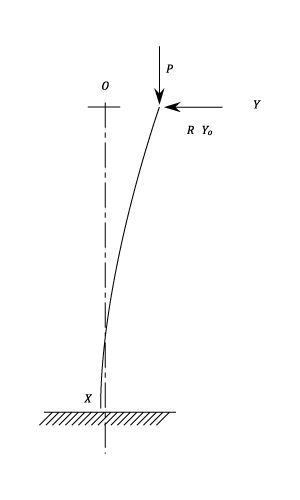
Problem

A Strut of length l is encased at it's lower end. The upper end is elastically supported against lateral deflection so that the resisting force is k times the end deflection. Show that the crippling load is given by: