Torsion

The relationship between torsional forces, shear strain and polar moments of inertia.

View other versions (4)

Contents

Introduction
Circular Shafts
Shafts Of Varying Diameter
Composite Shafts
Combined Bending And Twisting.
Strain Energy In Torsion.
Moments Of Inertia
Page Comments

Introduction

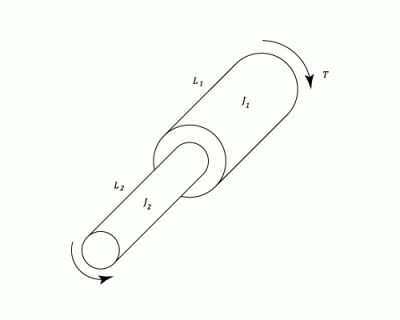
Torsion occurs when an object, such as a bar with a cylindrical or square cross section (as shown in the figure), is twisted. The twisting force acting on the object is known as torque, and the resulting stress is known as Shear stress. If the object undergoes deformation as a result of and in the direction of the application of the force, the resulting deflection is known as Strain. Twisting a simple piece of blackboard chalk between ones fingers until it snaps is an example of a torsional force in action. A common example of torsion in engineering is when a transmission drive shaft (such as in an automobile) receives a turning force from its power source (the engine).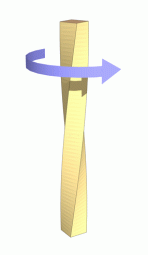

MISSING IMAGE!

23573/twisted_bar.png cannot be found in /users/23573/twisted_bar.png. Please contact the submission author.

Circular Shafts

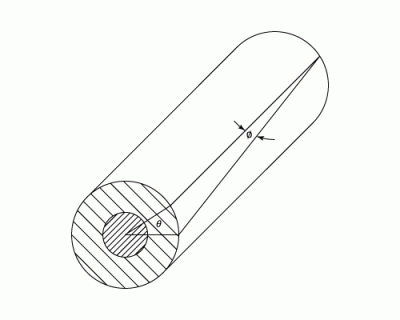
When a pure torque acts upon a shaft, shear stresses will be set up which act in directions perpendicular to the radius at all points.

The complimentary shear stresses on longitudinal planes will cause the distortion of filaments which were originally in the longitudinal direction. Assume that the points lying on a radius before twisting will remain on that radius, and that the angle of twist is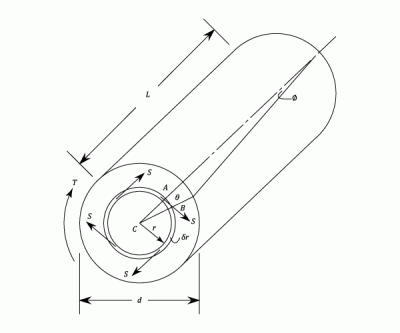 $\inline \theta$ uniformly over the length of the shaft.

MISSING IMAGE!

23287/Torsion-001.png cannot be found in /users/23287/Torsion-001.png. Please contact the submission author.

The diagram shows the shear strain $\inline \phi$ of elements which are at a distance r from the axis ( When T is constant $\inline \phi$ is constant). The original line OA has twisted to OB, and the angle ACB is now $\inline \theta$ , the relative angle of twist for cross sections a distance l apart .

$Arc\;\;AB = r\theta \, \;\approx \;l\phi$

(2)

But,

$\phi=\frac{s}{C}\;\;\;\;\;\;\;(\,C \;is\: the \:modulus\: of \;rigidity\,)$

(3)

From the above two equations

$\frac{s}{r} = \frac{C\,\theta }{l}$

(4)

The torque T can be equated to the sum of the moments of the tangential stresses on the element $\inline 2\, \pi \, r\, \delta r$

$\therefore\;\;\;\;\;\;T = \int s\, (2\pi rdr)\, r$

(5)

substituting from equation (3):

$T = \int \frac{C\, \theta }{l}(2\pi r^3)\, dr$

(6)

$= \frac{C\, \theta }{l}\;\frac{\pi r^4}{2}$

(7)

But the polar moment of inertia, J ,is

$J= \frac{\pi r^4}{2}$

(8)

Combing equations (3) and (6):

$\frac{T}{J} = \frac{s}{r} = \frac{C\, \theta }{l}$

(9)

This equation shows that the shear stress is proportional to the radius (the equation is analogous to that proven in the section on linear bending stress).

For a solid shaft $\inline J = \frac{\pi \, D^4}{32}$ and for a hollow shaft

$J = \frac{\pi}{32}(D^4 - d^4)$

(10)

The maximum stress for a solid shaft $\inline s_{max} = \frac{16\, T}{\pi \, D^3}\;\;at\;r = \frac{D}{2}$ and for a hollow shaft $\inline s_{max} = \frac{16\,D\,T}{\pi \, (D^4 - d^4)}\;\;\;\;at\;\;\frac{d}{2}$

Torsional stiffness $\inline \mu$ is defined as torque per radian twist. i.e.

$\mu =\frac{T}{\theta } = \frac{C\,J}{l}$

(11)

Example 1

Compare the weights of equal lengths of hollow and solid shaft to transmit a given torque for the same maximum shear stress, if the inside diameter is 2/3 of the outside.

From equation (7)

for a solid shaft:

$\frac{T}{\hat{s}} = \frac{2\,J}{D} = \frac{\pi \,D^3}{16}$

(12)

and

$\frac{T}{\hat{s}} = \frac{\pi (D_1^4 - d^4)}{16\,D_1}$

(13)

$\frac{\pi \,D_1^3}{16}(1 - \left(\frac{2}{3} \right)^4)$

(14)

If the torques on both shafts are equal

$D_1 = D\;.\sqrt[3]{\frac{81}{65}} = 1.075\,D$

(15)

The ratios of equal lengths = $\inline \frac{(D_1^2 - d^2)}{D^2} = \left(\frac{D_1}{D} \right)^2\left(1 - \frac{4}{9} \right)$

Thus the ratio of the weight of the hollow shaft to that of the solid shaft

$\left(\frac{5}{9} \right)\,1.075^2\; = 0.642$

(16)

Shafts Of Varying Diameter

MISSING IMAGE!

23287/Torsion-002.png cannot be found in /users/23287/Torsion-002.png. Please contact the submission author.

Angle of twist in larger shaft = $\inline \frac{T}{J_1}\;X\;\frac{l_1}{C_1}$ and for the thinner =

$\frac{T}{J_2}\;X\;\frac{l_2}{C_2}$

(17)

$\therefore\;\;\;\;Total\;twist\;\theta = T\left(\frac{l_1}{C_1J_1} + \frac{l_2}{C_2J_2} \right)$

(18)

If the shafts are made of the same material $\inline C_1 = C_2$

Composite Shafts

MISSING IMAGE!

23287/Torsion-003.png cannot be found in /users/23287/Torsion-003.png. Please contact the submission author.

The angle of twist per unit length is the same for both materials.

$\therefore\;\;\;Total\,\;T = T_s + T_b$

(19)

$but\;\;\;T_s = \frac{\theta \,C_s\,J_s}{l}\;\;\;\;and\;\;\;T_b = \frac{\theta \,C_b\.J_b}{l}$

(20)

$\therefore\;\;\;T = \frac{\theta }{l}\left(C_s\,J_s + C_b\,J_b \right)$

(21)

$\frac{\theta }{l} = \frac{T}{(C_s\,J_s + C_b\,J_b)}$

(22)

From which,

$t_s = \frac{C_s\,J_s}{C_s\,J_s + C_b\,J_b}\;T$

(23)

$t_b = \frac{C_b\,J_b}{C_s\,J_s + C_b\,J_b}\;.T$

(24)

$q_s = \frac{T_s}{J_s}\;X\;Radius_s$

(25)

$q_b = \frac{T_b}{J_b}\;X\;Radius_b$

(26)

Combined Bending And Twisting.

This occurs frequently in practice when a shaft is subjected to both bending and inertia forces. Stresses are set up due to gravity, torque, and shear forces, although the latter is usually unimportant since its maximum value occurs at the neutral axis where the bending stress is zero.

For the purposes of design it is necessary to calculate all the principle stresses( maximum shear stress, shear strain energy etc.) so that these can be used to compare them with the criterion of failure.

If $\inline f_b$ is the greatest bending stress and s is the greatest shear stress due to bending, then:

$f_b = \frac{32M}{\pi D^3}$

(27)

$s = \frac{16T}{\pi D^3}\;for\;a\;solid\;shaft$

(28)

For loading in the vertical plane, these stresses will occur together at the end of a vertical diameter, since there is no normal stress on longitudinal planes of the shaft, they are maximum principle stress.

$f_{max} = \frac{1}{2}\, f_b + \frac{1}{2}\sqrt{(f_b^2 + 4s^2)}$

(29)

$= \frac{16M}{\pi D^3} + \frac{1}{2}\sqrt{\left[\left( \frac{32M}{\pi D^3} \right)^2 + 4\left( \frac{16T}{\pi D^3} \right)^2 \right]}$

(30)

$\therefore\;\;\;\;f_{max} = \left(\frac{16}{\pi D^3} \right)\sqrt{(M^2 + T^2)}$

(31)

Note: that $\inline \frac{1}{2}[M + \sqrt{(M^2 + T^2)}]$ is the equivalent bending moment that would produce the same maximum stress.

The maximum shear stress q is given by;-

$q = \frac{1}{2}\sqrt{f_b^2\;+\a;4s^2}$

(32)

$\therefore\;\;\;\;q = \left(\frac{16}{\pi D^3} \right)\sqrt{(M^2 + T^2)}$

(33)

and this is the same shear stress as would be produced by a pure torque of magnitude $\inline \sqrt{(M^2 + T^2)}$

Example 2

A flywheel weighing 1200lb. is mounted on a shaft 3in. in diameter and midway between two bearings 24in. apart. If the shaft is transmitting 40 h.p. (1 h.p. = 550 ft.lb./sec)Calculate the maximum shear stress at the end of a vertical and horizontal diameter in a plane close to the flywheel.

$M = \frac{Wl}{4} = \frac{(1200\;X\;24)}{4}$

(34)

$= 7200\,lb.ft.$

(35)

$t = \frac{H.P.X\: 33000\: X\;12}{2\pi X}$

(36)

$= \frac{40\;X\;33000\;X\;12}{2\pi \;X\;360}\;\; = 7000lb.in$

(37)

At the ends of a vertical shaft use equation ( )

$Principle\;stress = \left(\frac{16}{\pi D^3}\right)\left(M\pm \sqrt{(M^2 + T^2)} \right)$

(38)

$= \left(\frac{16}{\pi \;X\;27} \right)\left(7200\pm \sqrt{(7200^2 + 7000^2} \right)$

(39)

$= 3250lb./sq.in.\;\;\;\;\;\;\;or\;\;\;\;\;\;\;-528lb./sq.in.$

(40)

thus on the "tension" side of the shaft the principle stresses are 3250 lb./sq.in. in tension and 528 lb./sq.in. compression. On the "Compression side the principle stresses are 3250lb./sq.in. in compression and 528lb./sq.in. in tension.

From equation ( ) the maximum shear stress is given by:-

$s_{max} = \left(\frac{16}{\pi D^3} \right)\sqrt{(M^2 + T^2)}$

(41)

$= 1890lb./sq.in.$

(42)

At the end of a horizontal diameter the bending stress is zero and the torsional shear stress has a value.

$\frac{16T}{\pi D^3} = 0.189\;X\;7000\;\; = 1320lb./sq.in.$

(43)

This is a pure shear stress and the principle stresses are $\inline \pm 1320 lb./sq.in.$ , the maximum shear stress being 1320 lb./sq.in.

Strain Energy In Torsion.

When a shaft of length l is gradually twisted through an angle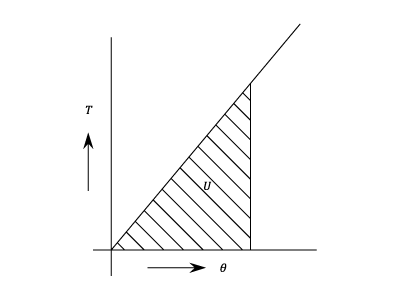 $\inline \theta$ under the influence of a Torque T. The work done (equals the total strain energy U) is given by:-

$U = \frac{1}{2}\: T\: \theta$

(44)

MISSING IMAGE!

23287/Torsion-004.png cannot be found in /users/23287/Torsion-004.png. Please contact the submission author.

Substituting value for T and $\inline \theta$ in equations (35)gives:-

$U = \frac{1}{2}\: \left(\frac{\pi D^3\,s_{max}}{16} \right)\;X\;\left(2s_{max}\: l \right)$

(45)

$= \left(\frac{s_{max}^2}{4C} \right)\;X\;\frac{\pi D^2l}{4}$

(46)

$= \left(\frac{s_{max}^2}{4C} \right)\;X\;volume$

(47)

This gives the total strain energy over the whole shaft. The shear stress varies from zero at the axis to $\inline s_{max}$ at the outside.

For a hollow tube :-

$U = \frac{1}{2}\left(\pi (D^4\,-\,d^4)s_{max} \right)\;X\;\frac{2\, s_{max}\: l}{CD}$

(48)

$\therefore\;\;\;U = \left(\frac{s_{max}^2}{4C} \right)\;X\;\left(\frac{(D^2\,+\,d^2)}{D^2} \right)\;X\;volume$

(49)

Example 3

A hollow shaft subject to a pure torque,attains a maximum shear stress of f. Given that the strain energy is $\inline \frac{f^2}{3C}$ calculate the ratio of shaft diameters.

From equation (35) above

$\frac{U}{Volume} = \left(\frac{f^2}{4C} \right)X\left(\frac{D^2 + d^2}{D^2} \right) = \frac{f^2}{3C}\;\;\;(given)$

(50)

$\frac{D^2 + d^2}{d^2} = \frac{4}{3}$

(51)

$From\;which\;\;\;\;\frac{D}{d} = 1.732$

(52)

Moments Of Inertia

MISSING IMAGE!

23287/Torsion-005.png cannot be found in /users/23287/Torsion-005.png. Please contact the submission author.