Engineering › Materials › Bending Stress ›

Moments of Inertia

Worked examples involving Bending Stess and Moments of Inertia.

View other versions (4)

Overview

Bending moment refers to the algebraic sum of all moments located between a cross section and one end of a structural member; a bending moment that bends the beam convex downward is positive, and one that bends it convex upward is negative.

The General Equation for bending is used throughout. The proof of this is to be found in "Engineering/Materials/Bending Stress". For convenience the equation is written here and is as follows:

$\frac{M}{I}=\frac{E}{R}=\frac{\sigma}{z}$

Where

is the Bending Moment
is the Moment of Inertia of the section
is Young's Modulus
is the Radius of curvature
$\sigma$ is the stress at a distance from the Neutral Axis

It is obviously important to use the same units throughout!

Example:

[imperial]

Example - Example 1

Problem

The beam of a symmetrical

section is simply supported over a span of 30 ft.

If the maximum permissible stress is 5 tons/sq.in., what concentrated load can be carried at a distance of 10 ft from one support?

Workings

Whilst it is not stated in the question, it is normal practice to load an

-section with

as the axis of bending. Thus the Bending Moment is in the

plane.

If the load is

tons then the maximum Bending Moment is given by: $\hat{M}=10\times\displaystyle\frac{2W}{3}$ or $20\times\displaystyle\frac{w}{3}$ i.e. Maximum Bending Moment = $\displaystyle\frac{20\;W}{3}\;ton - ft=80\;W\;ton - in$

Using the method for establishing the Moment of Area of an

-section beam shown in "Engineering/Materials/Bending"

$I =2 \left [4\times\frac{0.46^3}{12} + 4\times0.46(4.5 - \frac{0.46}{2})^2 \right] + \frac{(0.3\times8.08^3)}{12}$

$= 2 \left [0.032 + 33.4\right ] + 12.5 = 79.4\;in^4$

Using the General equation of Bending

$\frac{5}{4.5} = \frac{80\;W}{79.4}$

$\therefore\;\;\;\;\;W = \frac{(5\times79.4)}{(4.5\times80)} = 1.1\,tons$

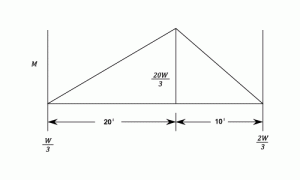
Solution

$W=1.1\;tons$