Gear Trains

An analysis of Gear Trains with particular reference to Epicyclic Gears.

View other versions (5)

Contents

Introduction
Gear Trains On Fixed Axes
Epicyclic Trains.
Page Comments

Introduction

Definitions

A gear train is a set or system of gears arranged to transfer rotational torque from one part of a mechanical system to another, with some gear ratio performing a mechanical advantage.

Epicyclic gearing or planetary gearing is a gear system consisting of one or more outer gears, or planet gears, revolving about a central, or sun gear.

Key Facts

Types of Gear Trains

Simple Train - three or more wheels connected in series.
Compound Train - an intermediate shaft carries two wheels connected in series.

The Structure of an Epicyclic gear - The Sun wheel, the planet wheels, the Annulus and the Spider.

Analysing epicyclic gear trains Three methods:

Tabular Method.
The Relative Velocity Method.
The Determination Of Torques.

One of the most common uses of Gear Trains is in the gear boxes of cars. In the simplest form, the crash gear box, a collection of spur gears were arranged to give different ratios of input to output speed and in the case of the reverse gear, change the direction of the output rotation.

The modern synchromesh gearbox is a development working on very similar principles.

MISSING IMAGE!

13108/img_0001_5.jpg cannot be found in /users/13108/img_0001_5.jpg. Please contact the submission author.

Another, and in many ways more interesting type of train uses epicyclic gears. Many modern cars use a small epicyclic in the starter motor but much larger and more complicated versions have been used as the main gearbox. Before the 1939 - 1945 war the Daimler Car Company used a "pre-selector" Wilson box.

In more recent years these were fitted to London Transport Buses and they were also to be found in some British Army armoured wheeled vehicles. The gear box, which is driven through a fluid fly wheel, allows the driver to pre-select the next gear to be used and then to make a very rapid change at the right moment. This ability is useful in heavy urban traffic and when driving across uneven country.

Gear Trains On Fixed Axes

The velocity ratio transmitted between two gears is the same as for two pitch circles rolling together. As the circular pitch must be the same for both wheels, the speed ratio is determined by the number of teeth.

i.e. $\inline \displaystyle\frac{n_A}{n_B} = \pm \;\displaystyle\frac{t_B}{t_A}$

The positive sign is taken for Internal gearing,
The negative sign is taken for External gearing.

A Simple train is one of three or wheels connected in series.

The gear ratio is independent of the size of the intermediate wheels which are called Idlers
For an odd number of externally geared wheels the direction of rotation of the last wheel is the same as the first.
For an even number of wheels the direction of rotation of the last wheel is opposite to that of the first.

A Compound Chains

When an intermediate shaft carries two wheels connected in series, the train becomes compound. For instance, if $\inline A$ gears with $\inline B$ , which is compounded with $\inline C$ , which then drives $\inline D$ .

i.e.

$\frac{n_A}{n_D} = \frac{t_B}{t_A}\times \frac{t_D}{t_C}$

(2)

Such arrangements can greatly increase or decrease the gear ratio.

Where the axis of the last wheel is in line with that of the first, the arrangement is known as a reverted train.

Epicyclic Trains.

One or more of the wheels of the gear train are now carried on an arm which itself rotates about the axis of the main wheels.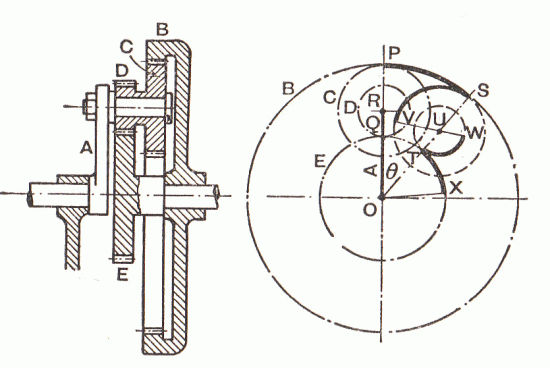

MISSING IMAGE!

13108/img_0002_3.jpg cannot be found in /users/13108/img_0002_3.jpg. Please contact the submission author.

The central main wheel is called the Sun wheel. The wheels carried by the arm are known as the Planet wheels and the outside internal wheel is called the Annulus. In some epicycilic gear trains the "arm" has a number of "limbs," each carrying a planet wheel. In these cases the "arm" may be referred to as the Spider.

There are a number of ways of analysing epicyclic gear trains. Three are described here:

Tabular Method

The first line of the table is obtained by fixing the arm and then giving one wheel (e.g. the wheel which is to be fixed later) one revolution.
Write down the corresponding revolutions of the other wheels from their number of teeth.
As all the wheels and the arm can be turned about the same axis, an equal number of revolutions may be added (or subtracted) from each wheel.
Any two lines may be multiplied (or divided) through by the same factor.
Any two lines may be combined. By these means the given conditions are satisfied and the resulting gear ratio can be determined.

Note. The above may seem confusing and should be read in conjunction with the worked examples; in particular Example (3).

The Relative Velocity Method

If the arm is fixed, then the gear becomes a simple or compound train. Thus the ratio of the speeds of any two wheels can be determined by using the methods of paragraph (2).

i.e.

$\frac{n_A - n_{arm}}{n_B - n_{arm}} = \frac{speed\;of\;A}{speed\;of\;B}$

(3)

(If the arm were fixed.)

Where there is an intermediate shaft between $\inline A$ and $\inline B$ carrying, two wheels $\inline C$ and $\inline D$ which are fixed together and arranged so that $\inline A$ drives $\inline C$ and $\inline D$ drives $\inline B$ , then the above equation can be modified to:

$\frac{(n_H - n_{arm})}{(n_B - n_{arm})} = \frac{t_C}{t_A}\times \frac{t_B}{t_D}$

(4)

which can be calculated from the number of teeth etc.

For simple epicyclic operating with a fixed annulus there is nothing to choose between the above two methods. However, if all the wheels are moving, or when dealing with compound epicyclic, the second method gives a quicker and more direct solution. A comparison of the methods can be made from Examples (3) and (4)

The Determination Of Torques

There are normally three torques acting on an epicyclic gear. These are:

$\inline \displaystyle \tau _1,$ the input Torque (in the sense of rotation of the input shaft)
$\inline \displaystyle \tau _0,$ the output torque (opposite to the sense of rotation of the output shaft)
$\inline \displaystyle \tau _C\;,$ the Torque on the casing.

Assuming the casing to be fixed, $\inline \eta \;\tau _1\;n_1 = \tau _0\;n_0$

From considerations of the power and for equilibrium ( Taking signs into account )

$\tau _1 + \tau _0 + \tau _1 = 0$

For input and output shafts to have the same direction of rotation

$\;\;\;\;\;\;\tau _C = \tau _0 + \tau _1$

(5)

(numerically)

For input and output to have opposite directions of rotation.

$\tau _C = \tau _0 + \tau _1$

(6)

(numerically)

When there is no fixed wheel there will, in general, be three torques to satisfy the following equations. Of the torques one can be found from the horse-power and speed.

$\tau _1 + \tau _2 + \tau _3 = 0$

And,

$\tau _1\;n_1 + \tau _2\;n_2 + \tau _3\;n_3 = 0$

Alternatively, the forces acting on each wheel (or compound pair) may be analysed separately since if the gear is running at constant speed, there is no resultant force and no resultant torque on any intermediate wheel.

Example:

[imperial]

Example - Example 1

Problem

Two shafts $A$ and $B$ in the same line are geared together through an intermediate parallel shaft $C$ . The wheels connecting $A$ and $C$ have a diametral pitch of 9 and those connecting $C$ and $B$ 4, the least number of teeth on any wheel being not less than 15. The speed of $B$ is to be about but not greater than $\displaystyle\frac{1}{12}$ the speed of $A$ and the ratio of each reduction is the same.

Find suitable wheels, the actual reduction and the distance of shaft $C$ from $A$ and $B$ .

Workings

Since the speed ratios between $A$ and $C$ and between $B$ and $C$ are to be the same and the overall reduction is greater than 12 then, using and adapting equation (1)

$\frac{n_A}{n_C} = \frac{n_C}{n_B}\;>\;\sqrt{12}$

i.e.

$\frac{n_A}{n_C} = \frac{n_C}{n_B}\;>\;3.47\;\;\;\;\;\;\;say\;\;3.5$

(1)

As $A$ and $B$ are in a straight line, the centre distance between each and $C$ must be the same. Also the diametral pitches are 9 and 4.

i.e. $\displaystyle\frac{t_A + t_{C1}}{2}\times 9 = \displaystyle\frac{t_{C2} + t_B}{2}\times4$

From the Speed Ratios $\displaystyle t_{C1} = 3.5\;t_A\;\;\;$ and $\;\;\;t_B = 3.5\;t_{C2}$

Substituting into equation (1), $t_A = \left (\displaystyle\frac{9}{4} \right )t_{C2}$ And $t_{C1} = \left (\displaystyle\frac{9}{4} \right )t_B$

It follows that $\displaystyle t_{C\,2}$ is the lesser and since it must be an even number greater than 15, try $\displaystyle t_{C\,2} = 16$ . Then $\displaystyle t_B = 56$ from the speed ratio.