Portal Frames
Bending Moments for Portal Frames
Introduction
Portal frame construction is a method of building and designing simple structures, primarily using steel or steel-reinforced precast concrete although they can also be constructed using laminated timber such as glulam.
The connections between the columns and the rafters are designed to be moment-resistant, i.e. they can carry bending forces.
A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.
Because of these very strong and rigid joints some of the bending moment in the rafters is transferred to the columns. This means that the size of the rafters can be reduced or the span can be increased for the same size rafters. This makes portal frames a very efficient construction technique to use for wide span buildings.
Portal frame construction is therefore typically seen in warehouses, barns and other places where large, open spaces are required at low cost and a pitched roof is acceptable.
Portal Frames.
The drawing shows a Portal Frame in which the ends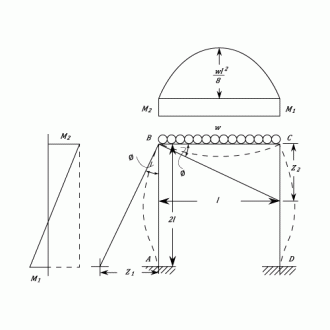
 Login
Login

